Rango de una función exponencial

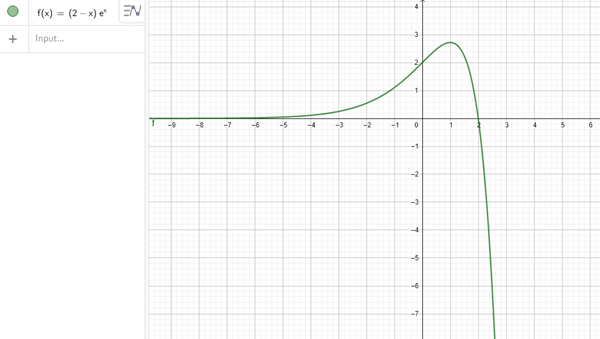
Primero se ve que la función es continua (composición de funciones continuas)

Luego veamos los límites cuando x tiende a +/- infinito

X --> -inf es una indeterminación del tipo 0 * infinito que si lo resuelves verás que tiende a 0

X --> + inf si lo resuelves verás que es - infinito

Ahora veamos la derivada

f'(x) = -e^x + (2-x) e^x = e^x (1 - x)

f'(x) = 0 --> x = 1 Si analizas el punto, verás que es un máximo local (y el único que tiene), así que veamos cuanto vale la función en dicho punto)

f(1) = (2-1) e^1 = e

Ya analizamos los límites y vimos cuanto vale la función en x=1 que es un máximo, por lo que el rango de esta función es (-inf, e]

Te dejo la gráfica donde se puede apreciar lo que digo