Calcule el área de la región limitada por f(×)=-3x/8(x-8) y g(x)=2x-3
Calcular el área de la región limitada por la parábola y la recta, realizar el proceso como el gráfico.
1 Respuesta
Respuesta
De la forma que lo escribiste, no queda claro cual es la función f(x), yo voy a asumir una (con "x-8" en el denominador) y en caso que no sea así, deberás ajustarlo.
Lo primero en estos casos, siempre que puedas es intentar hacer una gráfica de las funciones, para ver mejor que están pidiendo...
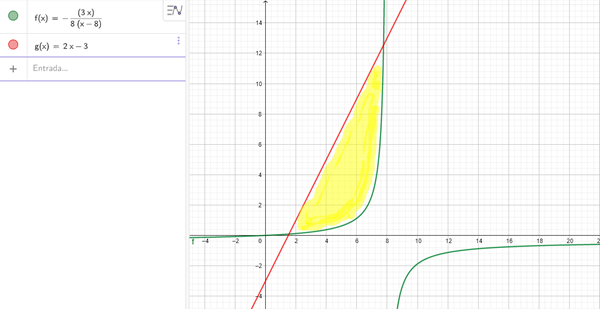
Se ve claramente que la función f(x) tiene una asíntota vertical en x=8, aunque igualmente el área que están pidiendo sería la que pinté yo donde g(x) está por arriba de f(x). Para ver cuales son los límites de integración, tenemos que ver donde se cortan ambas funciones, para eso hacemos f(x)=g(x)
$$\begin{align}&-\frac{3x}{8(x-8)}=2x-3\\&-3x=(2x-3)8(x-8)\\&-3x=16x^2-152x+192\\&0=16x^2-149x+192\\&\text{Planteo la resolvente...}\\&x_1=1.545 \land x_2=7.768\\&A = \int_{1.545}^{7.768}g(x)-f(x) dx = \int_{1.545}^{7.768}(2x-3)- (-\frac{3x}{8(x-8)}) dx = \\&\int_{1.545}^{7.768} 2x-3+\frac{3x}{8(x-8)} dx = \\&\int_{1.545}^{7.768} 2x-3 \ dx +\frac{3}{8} \int_{1.545}^{7.768} \frac{x}{x-8} dx =...\end{align}$$Te dejo la resolución de las integrales...
Salu2