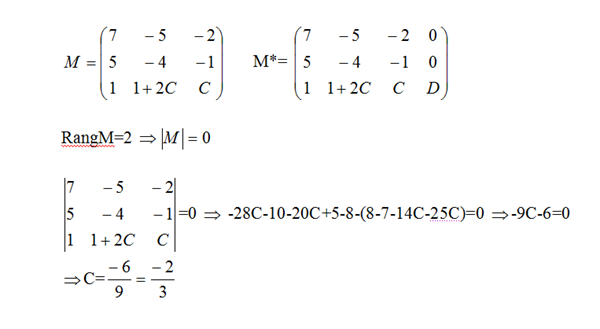Como hacer este ejercicio de planos que se interceptan?

Entiendo que quieres el 26 que es el único que habla de la intersección de tres planos, aunque lo que quiere es que la intersección sea conjunto vacío, o sea que no se intercepten los tres a la vez en algún punto.

Primero notamos que los dos planos dados no son paralelos entre sí ya que no tienen los coeficientes proporcionales. Y también, que el término independiente de ambos es D=0, luego los dos pasan por el origen de coordenadas. Por lo tanto para empezar nuestro plano buscado sera de la forma: Ax+By+Cz+D=0  (con D distinto de 0). Sin pérdida de generalidad hagamos A=1 ===> x+By+Cz+D=0  .

Como todos los puntos de la recta L han de estar a la misma distancia del plano buscado quiere decir que la recta y el plano han de ser paralelos.

Con lo cual el vector normal del plano y el vector de dirección de la recta han de ser perpendiculares, luego el producto escalar de estos vectores ha de ser cero:

$$\begin{align}&\vec{PQ}=Q-P=(-1,2,-1)-(-2,3,-3)=(1,-1,2)\\&\\&x+By+Cz+D=0  \Rightarrow \vec{n}=(1,B,C)\\&\\&\vec{PQ}·\vec{n}=(1,-1,2)·(1,B,C)=0 \Rightarrow 1-B+2C=0 \Rightarrow\\&B=1+2C\\&\\&\end{align}$$

Como la intersección de los tres planos es vacía quiere decir que el sistema formado por las tres ecuaciones de los planos ha de ser Incompatible, siendo la única posibilidad que

rangM=2    y  rangM*=3

Esto a su vez tiene dos subcasos:

Caso1: que haya dos planos paralelos y el otro secante a los dos

Caso2: que los tres planos se corten dos a dos,(pero no en la misma recta)

Estudiemos el Caso1: Como los dos planos dados no son paralelos querría decir que el plano buscado sería paralelo a uno de los dos.

Si es paralelo al primero sería de la forma:7x-5y-2z+D=0 , que a su vez tendría que ser perpendicular a L: (7,-5,-2)(1,-1,2)=7+5-4=8 (distinto de cero, no perpendicular)

Si es paralelo al segundo sería de la forma: 5x-4y-z+D=0, que a su vez tendría que ser perpendicular a L: (5,-4,-1)(1,-1,2)=5+4-2=7 (distinto de cero, no perpendicular).

Luego forzosamente estamos en el caso2: 

Planos secantes dos a dos ===> RangM=2    y  RangoM*=3

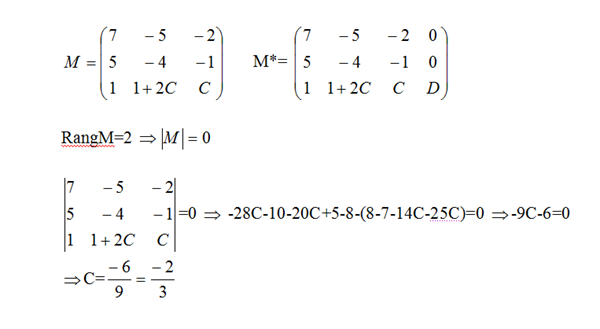
Tanto P como Q han de estar a la misma distancia del plano:

x+(1+2C)y+Cz+D=0

$$\begin{align}&dist(P,\pi)=\frac{|Ax_o+By_o+Cz_o+D|}{\sqrt{A^2+B^2+C^2}}\\&\\&P=(-2,3,-3)\\&\\&dist(P,\pi)=\sqrt{14}=\frac{|-2+(1+2C)3-3C+D|}{\sqrt{1^2+(1+2C)^2+C^2}}=\frac{|3C+D+1|}{\sqrt{1+(1+2C)^2+C^2}}\\&\\&Q=(-1,2,-1)\\&\\&dist(Q,\pi)=\sqrt{14}=\frac{|-1+(1+2C)2-C+D|}{\sqrt{1^2+(1+2C)^2+C^2}}=\frac{|3C+D+1|}{\sqrt{1+(1+2C)^2+C^2}}\\&\\&\Longrightarrow\\&|3C+D+1|=\sqrt{14}·\sqrt{1+(1+2C)^2+C^2}\\&\\&C=\frac{-2}{3}\\&\\&|3(\frac{-2}{3})+D+1|=\sqrt{14} · \sqrt{1+(1+\frac{-2}{3})^2+(\frac{-2}{3})^2}\\&\\&|D-1|=\sqrt{14}· \sqrt{1+\frac{1}{9}+\frac{4}{9}}\\&\\&|D-1|=\sqrt{14}·\sqrt{\frac{14}{9}} \Rightarrow |D-1|=\frac{14}{3} \Longrightarrow\\&\\&Si \ D-1>0\Rightarrow D-1=\frac{14}{3} \Rightarrow D=\frac{17}{3}\\&\\&Si \ D-1<0 \Rightarrow D-1=-\frac{14}{3} \Rightarrow D=-\frac{11}{3}\\&\\&Soluciones:\\&x-\frac{1}{3}y-\frac{2}{3}z+\frac{17}{3}=0 \Longrightarrow  3x-y-2z+17=0\\&\\&x-\frac{1}{3}y-\frac{2}{3}z-\frac{11}{3}=0 \Longrightarrow 3x-y-2z-11=0\\&\\&\end{align}$$

Saludos

:

: