¿Matemáticas como resuelvo el siguiente problema?
) Las ecuaciones de oferta y demanda para cierto producto son:
Oferta: 3q – 200p + 1800 = 0
Demanda: 3q + 100p – 1800 = 0
Donde p representa el precio por unidad en pesos y que el número de unidades por período.
- a) Gráfica ambas ecuaciones y encuentra el precio de equilibrio.
- b) Encuentra el precio de equilibrio cuando se fija un impuesto de 27 centavos por unidad al proveedor.
1 respuesta
Alfonso Gómez!
·
Son dos rectas, simplemente hay que graficarlas. Se toma la variable p en el eje Y y la variable q en el eje X.
Basta tener dos puntos de cada recta.
Para la oferta
3q – 200p + 1800 = 0
haciendo q=0 tenemos
-200p +1800 = 0
p =1800/200 = 9
luego tenemos el punto (0, 9)
y haciendo p=0 tenemos
3q + 1800 = 0
q = -1800 / 3 = -600
que nos da el punto (-600, 0)
·
Para la demanda
3q + 100p – 1800 = 0
haciendo q=0
100p - 1800 = 0
p = 1800/100 = 18
es el punto (0, 18)
Y haciendo p=0
3q -1800 = 0
q=1800/3 = 600
el punto es (600, 0)
Es una gráfica muy distinta en las proporciones del eje X e Y tendré que usar un programa especial que es más complicado que el habitual.
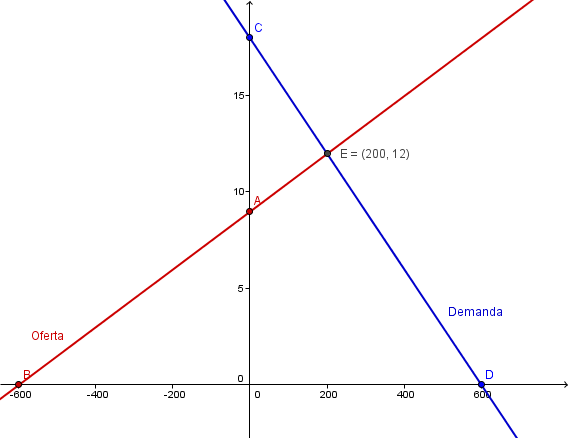
El propio programa se encargo de dar el punto de equilibrio E=(200, 12)
Pero lo normal es que lo tengamos que calcular nosotros a mano resolviendo el sistema de ecuciones, que tal como son lo que haremos es resta la primera a la segunda
3q – 200p + 1800 = 0
3q + 100p – 1800 = 0
-------------------------------
0q + 300p - 3600 = 0
300p = 3600
p = 3600 / 300 = 12
y ahora vamos a calcular q en la primera
3q - 200·12 + 1800 = 0
3q - 2400 + 1800 = 0
3q = 600
q=200
Con lo cual el punto de equilibrio es (200, 12)
·
b)
Si al proveedor le imponen un impuesto lo que va a hacer es repecurtirlo en el consumidor.
Vamos a despejar el precio en la ecuación de la oferta
3q – 200p + 1800 = 0
200p = 3q+1800
p = (3/200)q + 9
y este precio se verá incrementado en la cantía del impuesto
p= (3/200)q + 9 + 0.27
p = (3/200)q + 9.27
Y de nuevo a resolver esta ecuación y la de la demanda. Ahora sustituimos este valor de p en laecuación de la demanda
3q + 100[(3/200)q + 9.27] – 1800 = 0
3q + (3/2)q + 927 - 1800 = 0
(9/2)q - 873 = 0
(9/2)q = 873
q = (2/9)873 = 2·873/ 9 = 194
Y el valor de p será
p= (3/200)194 + 9.27 = 3·194/200 + 9.27 = 2.91 + 9.27 = 12.18
El punto de equlibrio será (194, 12.18)
Como podemos ver será más caro y se fabricarán menos unidades.
·
Y eso es todo.
buenísima, esta muy bien - n m
por que la q y la p son 0 - Alejandro Sanchez
Esa es la razón por la cual lo iguala a 0? - hola c.c
Porque lo igualas a 0?????? - hola c.c