Determine la longitud de arco de la gráfica f(x) = 9∛(x^2 ) en el intervalo [-1,8] y realice la gráfica.

;)
Hola Cristian!
Observa que la fórmula te la da con respecto dy, ya que con respecto de x quedaría una integral impropia

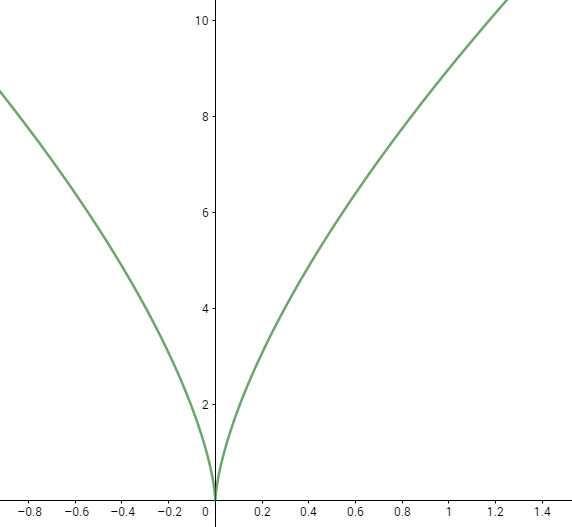
El gráfico es par, simétrico respecto el eje de ordenadas.

Calcularé dos veces la longitud de x=-1  a  x=0, y le sumaré la longitud de x=1 a x=8

Cambiemos la variable:

$$\begin{align}&y=9 x^{2/3}\\&y^3=9^3x^2\\&\\&x^2= \frac{y^3}{9^3}\\&\\&x= \frac{y^\frac 3 2}{9^\frac 3 2}\\&\\&x= \frac 1 {27} y^\frac 3 2\ ==>  \frac{dx}{dy}= \frac 1 {27}· \frac 3 2 y^\frac 1 2= \frac 1 {18} y^\frac 1 2\\&\\&Si\ x=-1==> y=9(-1)^\frac 2 3 =9\\&Si \ x=1==> y=9\\&\\&Si \ x=8==> y= 9·8^\frac 2 3=36\\&Si \ x=0==> y=0\\&\\&L=2 \int_0^9 \sqrt{1+ \Big(\frac 1 {18} y^\frac 1 2 \Big)^2}dy+ \int_9^{36}\sqrt{1+ \Big(\frac 1 {18} y^\frac 1 2 \Big)^2}dy=\\&\\&2 \Bigg[\frac{(y+324)^\frac 32}{27} \Bigg]_0^9 +  \Bigg[\frac{(y+324)^\frac 32}{27} \Bigg]_9^{36}=\\&\\&2(37 ^\frac 3 2-216)+(8·10^\frac 3 2-37^\frac 3 2)=\\&\\&\simeq29,73244\end{align}$$

Saludos y recuerda votar

||*||

;)