Calcular ├ dw/dt┤|_(t=0). Sustituyendo y derivando como una función de una variable
Regla de la cadena: una variable independiente
Sea w=x^2 y-y^2, x=sin(t), y=e^t. Calcular
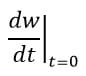
De las dos formas siguientes:
a. Sustituyendo y derivando como una función de una variable.
b. Aplicando la regla de la cadena
1 respuesta
Respuesta de Lucas m
1
;)
Hola Ume Lee!
a)
Sustituyendo:
$$\begin{align}&w=x^2y-y^2\\&x=sint\\&y=e^t\\&\\&w=\sin^2t·e^t-e^{2t}\\&\\&\frac{dw}{dt}=2sint·cost·e^t+\sin^2t·e^t-2e^{2t}\\&\\&\frac{dw}{dt}\Bigg|_{t=0}=0+0-2e^0=-2\\&\\&b)\\&\frac{dw}{dt}= \frac{dw}{dx}\frac{dx}{dt}+\frac{dw}{dy}\frac{dy}{dt}=2xy·cost+(x^2-2y)e^t\\&\\&t=0\\&\\&x(0)=sin0=0\\&y(0)=e^0=1\\&\\&\frac{dw}{dt}\Bigg|_{t=0}=0+(0-2)e^0=-2\end{align}$$Saludos
;)
||*||
