Desde el punto C, el ángulo de elevación de la cima A de una peña es de 51°.
Geometría
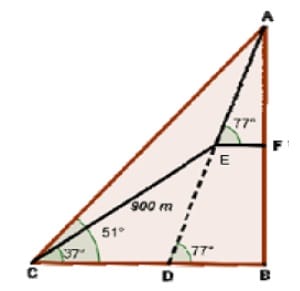
Desde el punto C, el ángulo de elevación de la cima A de una peña es de 51° (ver figura). Después de subir 900 metros por la rampa CE, inclinada 37° con la horizontal, se llega al punto E desde el que la peña se ve bajo un ángulo de 77°. Con esos datos, se pide calcular la altura AB de la peña. Suponer que AB⊥CB.
1 respuesta
Respuesta de Lucas m
1
;)
Hola Karla!
Hay diferentes caminos. Yo calcularé AC, y luego utilizaré el triángulo rectángulo ABC.
Para calcular AC usaré el triángulo obtusángulo ACE, del que conocemos EC=900 m. Calculemos sus ángulos:
Angulo CAB=90º-51º=39º
Angulo EAF=90º-77º=13º
Angulo CAE=Angulo CAB- AnguloEAF=39º-13º=26º
Angulo ACE=51º-37º=14º
Triángulo CAE ==> Angulo CEA=180º-14º-26º=140º y aplicando Teorema del seno:
$$\begin{align}&\frac{CE}{senCAE}=\frac{AC}{sen CAE}\\&\\&\frac{900}{sen 26º}=\frac{AC}{sen140º}\\&\\&AC=\frac{900 sen 140º}{sen26º}\\&\\&Triángulo\ Rectángulo \ ABC:\\&\\&sen51º= \frac{AB}{AC}\\&\\&AB=ACsen51º=\frac{900 sen 140º·sen51º}{sen26º}=1025.5826\ \ m\end{align}$$
