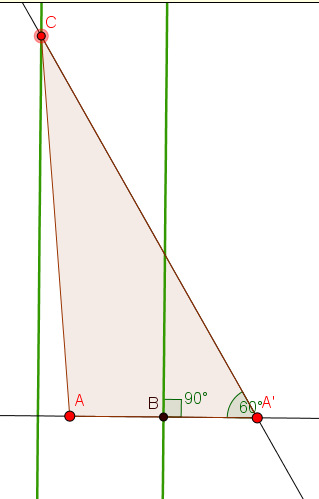
Dadas dos rectas paralelas y un punto en el “interior” de ambas rectas, hallar un triángulo que tenga un ángulo de 60°
Geometría
Dadas dos rectas paralelas y un punto en el “interior” de ambas rectas, hallar un triángulo que tenga un ángulo de 60° y para el cual el punto es uno de sus vértices, una de las rectas es una altura y la otra es una mediatriz.
1 Respuesta
;)
Hola karla!
Construcción:
Sean en verde las paralelas (altura y mediatriz) y A el punto interior.
Si una verde es la altura significa que la base es perpendicular:
Dibuja por A una perpendicular a las verdes.
Una recta quedará dentro y otra fuera del rectángulo. Como la mediatriz va por dentro dibuja el simétrico de A respecto la que quieres que sea la mediatriz (la de la derecha por ejemplo):obtendras A' (es elsegundo vértice). El punto B te sirve para dibujar el simétrico.
Por A' dibuja un ángulo de 60º y traza la recta oblicua que cortará a la verde de la izquierda
En el tercer vértice C
Saludos
;)
;)
