Calcular área en el Folium de Descartes

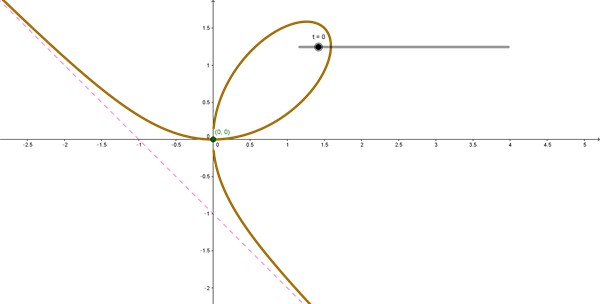
Yo no sé como lo habrás integrado, pero yo he pensado que lo mejor es pasar la curva a polares.

$$\begin{align}&r= \sqrt{\left(\frac{3t}{1+t^3}  \right)^2+\left(\frac{3t^2}{1+t^3}  \right)^2}=\frac{3t \sqrt{1+t^2}}{1+t^3}\\&\\&\theta=arctg\, t\implies t=tg\,\theta\\&\\&r=\frac{3tg\theta \sqrt{1+tg^2 \theta}}{1+tg^3\theta}=\frac{3 sen\theta}{\cos\theta\left(1+\frac{sen^3\theta}{\cos^3\theta}  \right)\cos\theta}\\&\\&r=\frac{3 sen\theta\, \cos\theta}{\cos^3\theta+sen^3\theta}\\&\\&\text{La giro 45º para que sea fácilmente calculable}\\&\text{después la ecuación de la asíntota}\\&\\&r=\frac{3 sen\left(\theta-\frac \pi 4\right)\, \cos\left(\theta-\frac \pi 4\right)}{\cos^3\left(\theta-\frac \pi 4\right)+sen^3\left(\theta-\frac \pi 4\right)}\\&\\&\text{El bucle es la curva entre }\frac{\pi}4\le\theta\le \frac {3\pi}{4}\\&\text{Las ramas entre }\frac{3\pi}4\le\theta\le \frac {5\pi}{4}\\&\\&\text{La asíntota convertida ahora en horizontal es}\\&r=-\frac{\sqrt 2}{2\,sen\,t}\\&\\&\text{Tomada lo mismo que las ramas, entre }\frac{3\pi}4\le\theta\le \frac {5\pi}{4}\\&\text{le falta el segmento en el centro de longitud } \sqrt 2\\&\\&\end{align}$$

No he mirado cómo se podría hacer bonito en Goegebra, yo lo he hecho con Winplot que me manejo rápido con él

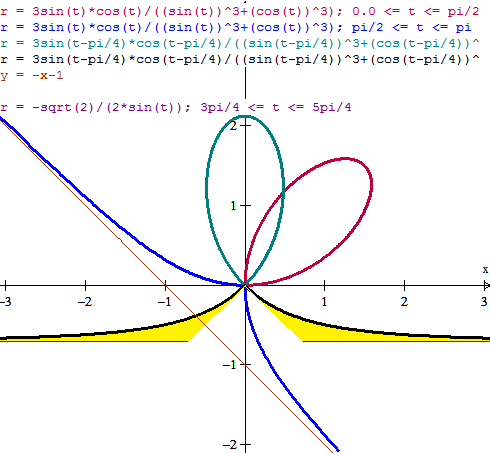
Y ahora es cuestión de aplicar la formula para calcular él area en polares.

$$\begin{align}&A=\frac 12\int r^2\;d\theta\\&\\&\text{Para el bucle, la calculo si}\text{n girar, que lo había}\\&\text{hecho así al principio y es más corto de escribir}\\&\\&A=\frac 12\int_0^{\frac \pi 2}\left(\frac{3 sen\,t ·\cos t}{sen^3t+\cos^3t}\right)^2\;d\theta=1.5\\&\\&\text{La hice con WolframAlpha}\\&\\&\end{align}$$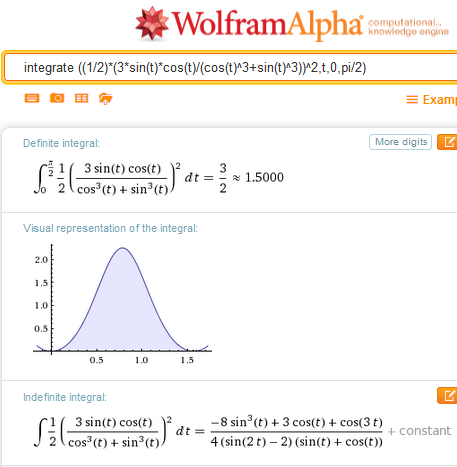

Y para el área entre las ramas y la asíntota hay que aplicar la formula a las dos curvas y restar

$$\begin{align}&A= \frac 12\int _{3\pi/4}^{5\pi/4}\left[\left(\frac{\sqrt 2}{2 sen\theta}\right)^2-\left(\frac{3 sen\left(\theta-\frac \pi 4\right)\, \cos\left(\theta-\frac \pi 4\right)}{\cos^3\left(\theta-\frac \pi 4\right)+sen^3\left(\theta-\frac \pi 4\right)}\right)^2\right]d\theta=1\end{align}$$

Y esto hecho con WolframAlpha fue

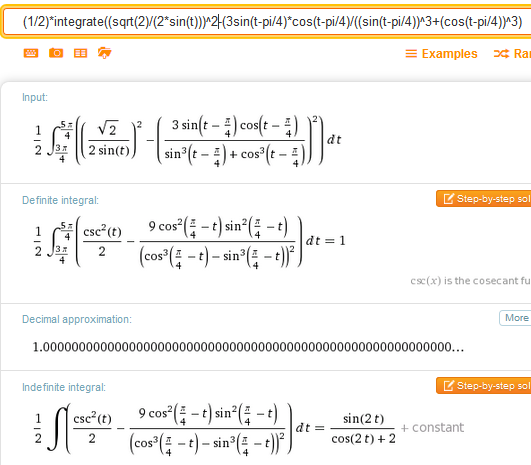
Y hay que añadir el área del triángulo que falta en la imagen, es un triángulo de base sqrt(2) y de altura sqrt(2)/2 luego es

A=1/2

Con lo cual el área entre ramas y asíntota es 1+ 1/2 = 3/2 = 1.5 la misma que el bucle.

Y eso es todo, sa lu dos.

:

: