Dos cantidades están en proporción áurea (o sección áurea) cuando al dividir una de la otra da el número áureo, que se representa con la letra griega phi).
Para demostrar esto utilizaré una relación conocida y es que el cos36=phi/2
También necesitaré la fórmula trigonométrica del ángulo mitad.
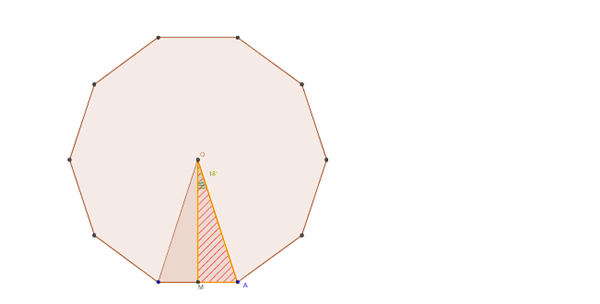
Vamos allà:
$$\begin{align}&Número \ áureo\\&\phi=\frac{1+\sqrt 5}{2}\\&\\&cos36º=\frac{\phi}{2}\\&\\&\sin(\frac{\alpha}{2})=\sqrt{\frac{1-\cos \alpha}{2}}\\&\\&\\&En \ el \ triangulo \ rayado:\\&\\&sin18º=\frac{l/2}{r} \Longrightarrow \frac{r}{l}=\frac{1}{2sin18º}\\&\\&sin18º=\sin(\frac{36º}{2})=\sqrt{\frac{1-cos36}{2}}=\sqrt{\frac{1- \frac{\phi}{2}}{2}}=\sqrt{\frac{2- \phi}{4}}=\frac{1}{2} \sqrt{2- \phi}\\&\\&\sqrt{2- \phi}=\sqrt{2-\frac{1+\sqrt 5}{2}}=\sqrt{\frac{3- \sqrt 5} {2}}=\frac{1}{\sqrt 2} \sqrt{3- \sqrt 5}\\&\\&Separando \ raíces:\\&\sqrt{{3- \sqrt 5} }=\sqrt x -\sqrt y \Rightarrow elevando \ al \ cuadrado\\&\\&3-\sqrt 5=x+y-2 \sqrt x \sqrt y \Longrightarrow Igualando \ partes \ enteras \ y \ radicales:\\&3=x+y\\&\sqrt 5=2 \sqrt x \sqrt y \Rightarrow 5=4xy\\&Resolviendo \ el \ sistema\\&y=3-x\\&5=4x(3-x) \Rightarrow 4x^2-12x+5=0 \Rightarrow\\&x=\frac{5}{2}\\&y= \frac{1}{2}\\&\\&\Longrightarrow\\&sin18º=\frac{1}{2} \sqrt{2- \phi}=\frac{1}{2}\frac{1}{\sqrt 2}(\sqrt{\frac{5}{2}}-\sqrt{ \frac{1}{2}})=\frac{1}{4}(\sqrt 5 -1)\\&\\&Luego:\\&\\&\frac{r}{l}=\frac{1}{2 \sin 18º}=\frac{1}{2 \frac{1}{4}(\sqrt 5 -1)}=\frac{2}{\sqrt 5 -1}=Racionalizando\\&\\&\frac{2}{\sqrt 5 -1}·\frac{ \sqrt 5 +1}{\sqrt 5 +1}=\frac{2(\sqrt 5 +1)}{5-1}=\frac{\sqrt 5 +1}{2}=\phi\\&\\&c.q.d º (como \ queríamos \ demostar)\\&\\&\end{align}$$Faltaría demostrar el valor del cos36º (pero lo puedes comprobar con la calculadora)


Exacto Gustavo........( como te acuerdas de todo eso ???.......) - albert buscapolos Ing°
Perdon...quise decir Lucas mm................... - albert buscapolos Ing°
Me gusta la geometría y he leido sobre la propoción aureahttp://www.bdigital.unal.edu.co/39511/1/15033846.2014.pdf http://gaussianos.com/una-inesperada-aparicion-del-numero-aureo/ Saludos - Lucas m