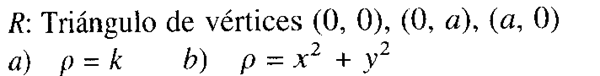Hallar el centro de masa de la lámina cuya densidad se específica

---

---

¡Hola Francisco!

·

El triángulo está bien claro, es un triangulo rectángulo con los catetos sobre los ejes y la hipotenusa formando 45º con ellos.

La ecuación de la hipotenusa se dedude fácilmente, es:

y = -x+a

Las coordenadas del centro de masas son

$$\begin{align}&x_c=\frac{\iint_Dx· \gamma(x,y)\; dy\,dx}{\iint_D\gamma\;dy\;dx}\\&\\&y_c=\frac{\iint_Dy· \gamma(x,y)\; dy\,dx}{\iint_D\gamma\;dy\;dx}\\&\\&\\&\\&\text{Cuando }\gamma(x,y)=k\\&\\&\int_0^a\int_0^{-x+a}k\; dy\,dx =\\&\\&k\int_0^ay\bigg|_0^{-x+a}dx =\\&\\&k\int_0^a(-x+a)dx=\\&\\&k·\left[-\frac{x^2}{2}+ax  \right]_0^a=\\&\\&k\left(-\frac{a^2}{2}+a^2  \right)=\frac{ka^2}{2}\\&\\&\\&\\&\int_0^a\int_0^{-x+a}kx \;dy\,dx=\\&\\&k\int_0^a x\int_0^{-x+a}dydx=\\&\\&k\int_0^ax\bigg[y  \bigg]_0^{-x+a}dx=\\&\\&k\int_0^ax(-x+a)dx=\\&\\&k\int_0^a(-x^2+ax)dx=\\&\\&k\left[-\frac {x^3}{3}+\frac{ax^2}{2}  \right]_0^{a}=\\&\\&k\left(-\frac{a^3}3+\frac{a^3}{2}  \right)=\\&\\&k·\frac{-2a^3+3a^3}{6}=k·\frac {a^3}6\\&\\&\\&\\&\int_0^a\int_0^{-x+a}ky\;dy\,dx=\\&\\&k\int_0^a \frac{y^2}{2}\bigg|_0^{-z+a}dx=\\&\\&\frac k2\int_0^a(x^2-2ax+a^2)dx=\\&\\&\frac k2\left[\frac {x^3}{3}-ax^2+a^2x  \right]_0^a\\&\\&\frac k2\left(\frac{a^3}{3}-a^3+a^3  \right)=\frac{ka^3}{6}\\&\\&\\&\\&x_c=\frac{\frac{ka^3}{6}}{\frac{ka^3}{2}}=\frac a3\\&\\&y_c=\frac{\frac{ka^3}{6}}{\frac{ka^3}{2}}=\frac a3\\&\\&\text{luego el centro de masas es}\\&\\&C_m=\left(\frac a3,\;\frac a3  \right)\end{align}$$

Y es todo, es sencillo pero lleva su trabajo.  Si quieres el ejercicio de la otra función de densidad mándalo en otra pregunta.