Respuesta
en
Matemáticas
a
Fórmula o método para calcular probabilidad
Me gustaría que Gustavo Omar Fellay viera si lo que voy a decir es correcto, porque el sabe más de estadística que yo (tampoco es que yo conozca mucho). Pienso que el ejercicio que planteas es un caso de distribución binomial con parametro= Y/100 La...
Respuesta
en
Matemáticas
y en 1 temas más
a
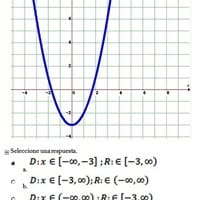
¿Cuál es el dominio y rango de la siguiente gráfica?
Respuesta
en
Matemáticas
a
Función cuadrática no me sale este problema
Si, el resultado que te da es correcto, no tiene raíces reales, la función no corta con el eje x en ningún punto
Respuesta
en
Matemáticas
y en 2 temas más
a
Calcular el valor del polinomio
El ejercicio es igual al otro. Para que el polinomio sea de grado 2, significa que el x^2 debe ser la mayor potencia de x, eso significa que el coeficiente del x^3 debe ser cero. A partir de ahí es el mismo procedimiento, que creo puedes hacer
Respuesta
en
Matemáticas
y en 2 temas más
a
Como calculo el coeficiente principal de este polinomio
Entonces el resultado que tienes de a=7 es correcto
Respuesta
en
Física
a
Que significa W=Ecf-Ec0 = ∆Ec
W es el trabajo, la segunda igualdad es energía cinética final menos la inicial, y el triangulo que se llama delta representa la variación de energía cinética (otra forma de decir energía cinética final menos la inicial)
Respuesta
en
Matemáticas
y en 2 temas más
a
Una matriz cuadrada A se llama nilpotente si existe un entero positivio m tal que Asea A^m=0
Respuesta
en
Matemáticas
y en 2 temas más
a
Sea A una matriz invertible de orden nxn tal que A^-1=2^T demuestre que dea(A^2)= 1/2^n
Respuesta
en
Matemáticas
y en 2 temas más
a
Geometría vectorial Demuestre que si A es invertible y simétrica, entonces A^-1 es simétrica
Si una matriz es simétrica entonces A=A^t Empecemos en AA^-1=I (AA^-1)^t=I^t (A^-1)^t(A)^t=I Por la propiedad que puse en la primera línea (A^-1)^t.A=I Entonces (A^-1)^t es la inversa de A, pero la inversa de una matriz es única entonces...
Respuesta
en
Matemáticas
y en 2 temas más
a
Geometría vectorial, una matriz A tal que A^2=A se llama idempotente .
Si se cumple que A^2=A, entonces det(A^2)=det(A). Nota: El det(A.B)=det(A).det(B) Det(A^2)-det(A)=0 Det(A)(Det(A)-1)=0 De ahí vemos que puede ser 0 o 1