Demostrar informalmente que el sólido de revolución mostrado en la siguiente figura, es;
Análisis de la integral doble
Demostrar informalmente que el sólido de revolución mostrado en la siguiente figura, es;
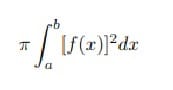

1 Respuesta
Respuesta de Norberto Pesce
2

