Encuentre el lugar geométrico de los puntos P(x,y) cuyo producto de las pendientes de la recta que unen P(x,y)

;)
Hola karla!
Sean P=(x, y) los puntos del plano que han de verificar esa propiedad.

Pendiente recta AP:

$$\begin{align}&m_{AP}=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}=\frac{y-(-2)}{x-3}= \frac {y+2}{x-3}\\&\\&\\&m_{BP}=\frac{y-1}{x+2}\\&\\&m_{AP}·m_{BP}=-6\\&\\&\frac {y+2}{x-3}·\frac{y-1}{x+2}=-6\\&\\&\frac{y^2+y-2}{x^2-x-6}=-6\\&\\&y^2+y-2=-6(x^2-x-6)\\&\\&\\&(y^2+y)-2=-6[(x^2-x)-6]\\&\text{Completando cuadrados,esos binomios vienen de los siguientes cuadrados:}\\&y^2+y=(y+ \frac 1 2)^2- \frac 1 4\\&\\&x^2-x=(x-\frac 1 2)^2- \frac 1 4\\&\\&La \ curva \ queda:\\&(y+ \frac 1 2)^2- \frac 1 4-2=-6 \Big[(x- \frac 1 2)^2- \frac 1 4-6\Big]\\&\\&(y+ \frac 1 2)^2+6(x-\frac 1 2)^2=\frac 6 4+36+ \frac 1 4+2\\&\\&(y+ \frac 1 2)^2+6(x-\frac 1 2)^2=\frac{159}4\\&\\&Dividiendo\ por \ \frac{159} 4\\&\\&\frac{(y+ \frac 1 2)^2}{\frac{159}4}+\frac{6(x-\frac 1 2)^2}{\frac{159}4}=1\\&\\&\frac{(y+ \frac 1 2)^2}{\frac{159}4}+\frac{(x-\frac 1 2)^2}{\frac{159}{24}}=1\\&\\&\frac{159} 4> \frac{159}{24}\\&\\&\text{Es una elipse vertical}\\&\\&\\&\\&\end{align}$$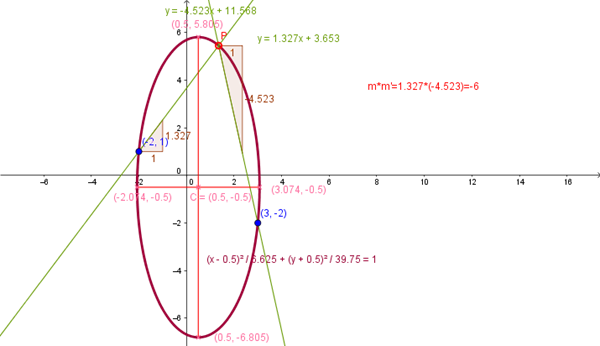

Saludos

;)

;)