Demostrar que la ecuación 〖7x〗^2-49x-14y+135=0, Representa una parábola. Determine:

;)
Hola Omar!

Completando cuadrados:

$$\begin{align}&7x^2-49x+14y+135=0\\&\\&7(x- \frac 7 2)^2- \frac{49} 4 7=-14y-135\\&\\&7(x- \frac 7 2)^2=-14y-135+\frac{343}4\\&\\&7(x- \frac 7 2)^2=-14y - \frac {197}4\\&\\&(x- \frac 7 2)^2=-2y- \frac{197}{28}\\&\\&(x- \frac 7 2)^2=-2(y+\frac {197}{56})\\&\\&parábola \ tipo:\\&(x-h)^2=4p(y-k)\\&p<0\\&4p=-2\\&p=-\frac 1 2\\&\\&parábola \ desplazada \ con \ eje \ vertical \ x= \frac 7 2=3.5\\&\\&V=(\frac 7 2, - \frac{197}{56})\\&directriz:\ \ y=-p-k=\frac 1 2-  \frac{197}{56}=- \frac{169}{56}\\&\\&y=- \frac{169}{56}=-3.0179\\&\\&Foco:\\&(\frac 7 2 ,p-k)=(\frac 7 2, -\frac 1 2- \frac{197}{56})=( \frac 7 2,- \frac{225}{56})=(3.5,-4.0179)\\&\end{align}$$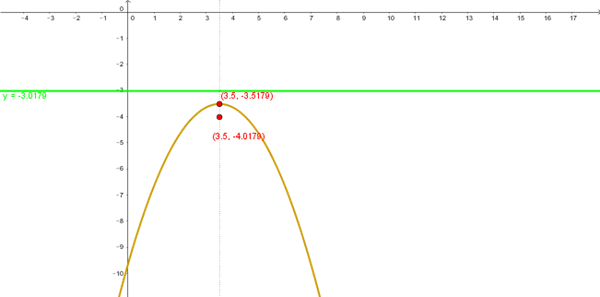

SAludos

;)

;)