Problema 3. Demostrar que : x^2+〖5y〗^2+5x+25y=100 es la ecuación de una elipse y determine: Centro Focos Vértices
Buenas noches me podrían colaborar por favor con la solución de este ejercicio
1 respuesta
Respuesta de Lucas m
1
;)
Hola Omar!
Completando cuadrados:
$$\begin{align}&x^2+5x+5(y^2+5y)=100\\&\\&(x+ \frac 5 2)^2- \frac{25} 4+5(y+\frac 5 2)^2-5· \frac {25} 4=100\\&\\&\\&(x+ \frac 5 2)^2+5(y+ \frac 5 2)^2=100+ \frac{25} 4+\frac{125} 4\\&\\&(x+ \frac 5 2)^2+5(y+ \frac 5 2)^2=\frac{275} 2\\&\\&dividiendo \ por \ \frac{275} 2\\&\\&\frac{(x+ \frac 5 2)^2}{\frac{275} 2}+\frac{5(y+ \frac 5 2)^2}{\frac{275} 2}=1\\&\\&\frac{(x+ \frac 5 2)^2}{\frac{275} 2}+\frac{(y+ \frac 5 2)^2}{\frac{55} 2}=1\\&\\&elipse \ horizontal \ centrada \ en (- \frac 5 2, - \frac 5 2)\\&\\&a^2=b^2+c^2\\&\\&c^2= \frac{275} 2 - \frac {55} 2=110\\&\\&c= \sqrt{110}\\&\\&Focos\\&\Big( \sqrt{110} -\frac 5 2,-\frac 5 2 \Big)=(7.99,-2.5)\\&\\&\Big( -\sqrt{110} -\frac 5 2,-\frac 5 2 \Big)=(-12.99,-2.5)\\&\\&Vertices:\\&\\&\Big( \sqrt{ \frac{275} 2}-\frac 5 2, -\frac 5 2 \Bigg)=(9.226,-2.5)\\&\\&\\&\Big( -\sqrt{ \frac{275} 2}-\frac 5 2, -\frac 5 2 \Bigg)=(-14.226,-2.5)\\&\\&\Big(-\frac 52, \sqrt{\frac {55} 2}- \frac 5 2 \Big)=(-2.5,2.744)\\&\\&\Big(-\frac 52, -\sqrt{\frac {55} 2}- \frac 5 2 \Big)=(-2.5,-7.744)\end{align}$$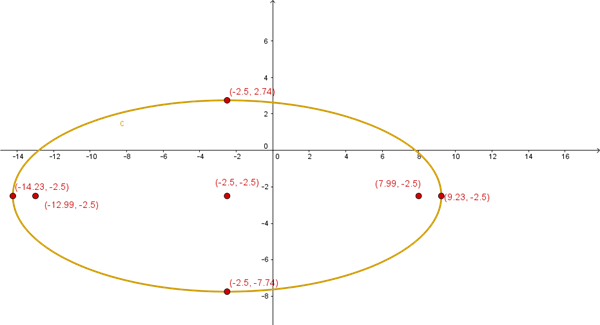
Saludos
;)
;)
