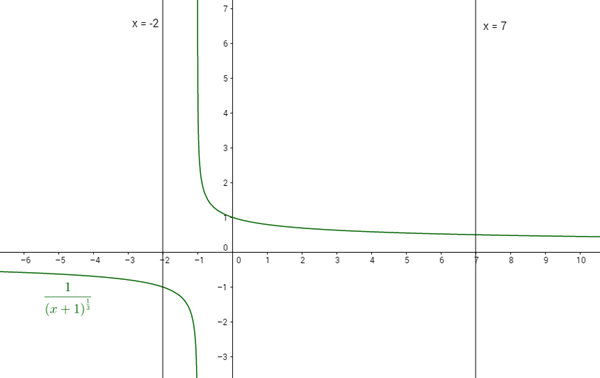
Quien puede resolver ejercicios sobre integrales convergentes o divergentes
Evaluar las siguientes integrales impropias si convergen o divergen:
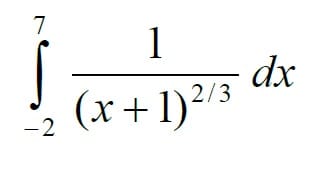
Amigos de todoexpertos les pido su colaboración en la solución de este problema, de igual forma especificar si el ejercicio es convergente o divergente.
1 respuesta
Respuesta
1
Como el intervalo incluye al -1 que es donde la función se indetermina, hay que calcularla partiendo la integral
$$\begin{align}&\int_{-2}^{7} \frac{1}{(x+1)^{2/3}}dx = \lim_{L \to -1} \int_{-2}^{L} (x+1)^{-2/3}dx + \lim_{L \to -1} \int_{L}^{7} (x+1)^{-2/3}dx = \\&\lim_{L \to -1} \frac{(x+1)^{-1/3}}{-1/3} \bigg|_{-2}^{L} + \lim_{L \to -1} \frac{(x+1)^{-1/3}}{-1/3} \bigg|_{L}^{7}=\\&\lim_{L \to -1} -3 \bigg(\frac{1}{(L+1)^{1/3}}-\frac{1}{(-2+1)^{1/3}} \bigg) +\lim_{L \to -1} -3 \bigg(\frac{1}{(7+1)^{1/3}}-\frac{1}{(L+1)^{1/3}} \bigg) =\\&-3 \bigg( \lim_{L \to -1} \frac{1}{(L+1)^{1/3}}+1 + \frac{1}{2}-\lim_{L \to -1} \frac{1}{(L+1)^{1/3}} \bigg) =\\&-3 \bigg( \frac{3}{2} \bigg) =-\frac{9}2\end{align}$$Te dejo la gráfica de la función
Salu2