2 respuestas
·
·
¡H o l a Alex!
No es cuestión de que puntues de cualquier manera. Responder preguntas lleva un trabajo, mientras que buscar un enlace en internet poniendo una palabra y pegarlo no lleva ningún trabajo y se puede hacer sin tener ni puta idea de la pregunta, que a veces ni se la lee entera.
Es por eso que yo no quiero contestarte por esto que hiciste aquí y lo sabes:
Como resuelvo este ejercicio de limites (puntos extremos , inflexión)
Si ese es el tipo de respuestas que valoras, no te mereces las respuestas de los expertos de verdad, y es una ofensa para nosotros ver esa puntuación gratuita que le diste al entrometido y falso experto de Jorge Herrera, y yo mientras vea esos puntos no contestaré preguntas tuya.
S a l u d o s.
-----
-----
ya elimine esos puntos no sabia que esa persona se dedicaba a hacer eso, respeto el esfuerzo que los verdaderos expertos demuestran en sus respuestas
Yo ya llevaba varios advirtiendo sobre él en mi perfil, pensaba que lo habrías visto. Si vas a su perfil, a sus respuestas y miras las respuestas que ha dado en matemáticas verás que no ha resulelto ni un problema ni medio, vamos, que no ha derivado ni e^x ni ha sumado dos números. Pones a un niño de 12 años y lo hace mejor que él.
En un momento me pongo con el problema.
S a l u d o s.
Tienes que calcular la función de coste en función de las millas sobre tierra, que no son las que marca como x en el dibujo, las millas sobre tierra son las otras, esto que quede bien claro
O sea, que yo llamo x al tramo de tierra desde los tanques hasta que me meto bajo el pantano.
Y las millas bajo el pantano aplicando el teorema de Pitágoras serán:
$$\begin{align}&m_p=\sqrt{(4-x)^2+4^2}\\&\text{mejor poner}\\&m_p= \sqrt{(x-4)^2+16}\\&\\&\text{Con lo cual la función costo es}\\&\\&f(x)=20000x+25000 \sqrt{(x-4)^2+16}\\&\\&\text{La derivamos e igualamos a 0}\\&\\&f'(x)=20000+\frac{25000·2·(x-4)}{2 \sqrt{(x-4)^2+16}}=0\\&\\&\frac{25000·(x-4)}{\sqrt{(x-4)^2+16}}=-20000\\&\\&5(x-4)=-4 \sqrt{(x-4)^2+16}\\&\\& 25(x-4)^2=16(x-4)^2+256\\&\\&9(x-4)^2=256\\&\\&(x-4)^2= \frac{256}{9}\\&\\&x-4 = \pm \frac {16}3\\&\\&x = 4\pm \frac{16}3\\&\\&x= -\frac 43 \quad y\quad \frac{28}3\\&\\&\text{¡¡¡ Pero cuidado!!!}\\&\\&\frac {28}3 \text { es una respuesta fantasma, verifica la}\\&\text{ecuación tras elevar al cuadrado, pero no verifica}\\&\\&\frac{25000·(x-4)}{\sqrt{(x-4)^2+16}}=-20000\\&\\&\text{luego no sirve}\\&\\&\text{Y }-\frac 43 \text{ tampoco sirve, ya que f(x) solo}\\&\text{está pensada }x\ge 0\quad\text{ Si x es negativa la}\\&\text{función debería ser}\\&\\&f(x)=-20000x+25000 \sqrt{(x-4)^2+16}\\&\text{y las soluciones son las mismas, pero entonces}\\&\text{-4/3 sería la fantasma y 28/3 no serviría}\end{align}$$Resumiendo
Si x >= 0 no hay puntos críticos en [0, inf)
Si x<=0 no hay puntos críticos en (-inf, 0]
Y la función no es siempre creciente o decreciente sino que tiende a infinito por los dos infinitos, ¿Cómo puede ser que no haya puntos críticos?
Muy sencillo, la auténtica función de costo sería:
$$\begin{align}&f(x)=20000x+25000 \sqrt{(x-4)^2+16}\end{align}$$Y esta función no es derivable en x=0, eso es un punto crñitico de esos que nos solemos olvidar, y ahí es donde está el mínimo, pero la función no es derivable sino que hace un pico.
Luego la solución es x=0, es decir, que no se hace ni un solo metro sobre tierra, se hace todo el recorrido bajo pantano.
Todo este tiempo ha sido porque estaba desconcertado al principio porque no diera respuestas en [0, 4] que creía sería lo lógico.
Y eso es todo
S a l u d o s.
.
:
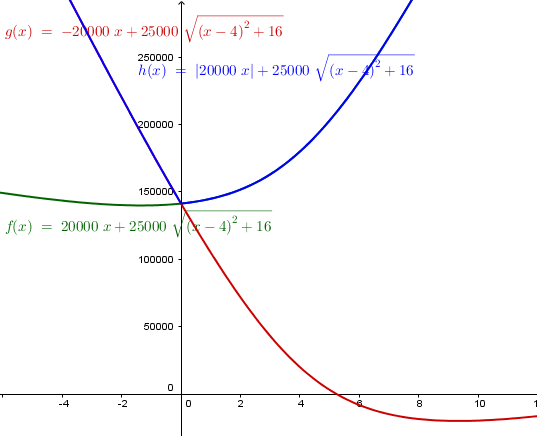
Espera, que se me olvido explicar un poco la grafica, tanto f(x) como g(x) son funciones suaves que representan el costo, f(x) cuando por tierra se avanza hacia la refinería y g(x) si se retrocede. Pero la autentica función es h(x) la azul que se superpone sobre la mitad de cada una y hace un pico.
¡Gracias!
Espera que no puse bien una cosa, la pensaba pero no la escribí bien.
Cuando decía la verdadera función de coste es esta
$$\begin{align}&f(x)=|20000x|+25000 \sqrt{(x-4)^2+16}\end{align}$$Y esa es de las que da poco gusto derivar y despejar porque hay que considerar dos casos que es más o menos lo que ya hice yo.
Y al final lo más sencillo es lo mejor, tal como ha hecho Lucas. Simplemente que primero hay que demostrar que fuera de [0,4] los costos son superiores a dentro de [0,4]
Recuerda que mi x no es la del dibujo sino lo de la izquierda. Pongo la función de costo verdadera para todo R.
$$\begin{align}&f(x)=|20000x|+25000·\sqrt{(x-4)^2+16}\\&\\&Si \;x\lt0\\&\\&x-4 \lt-4\\&\\&(x-4)^2\gt16\\&\\&f(x) > 0 +25000 \sqrt{16+16}=f(0)\\&\\&\\&\\&Si\; x \gt 4\\&\\&x-4\gt 0\\&\\&(x-4)^2 \gt 0 =(4-4)^2\\&\\&|20000x| \gt|20000·4|\\&\\&f(x)\gt|20000·4|+25000 \sqrt{(4-4)^2+16}= f(4)\end{align}$$Luego f(0) será menor que f(x) para x<0 y f(4) será menor que f(x) para x>4 por lo cual podemos calcular el mínimo de la función en todo R circunscribiéndonos al intervalo [0,4]
En ese intervalo cerrado ya vimos que no había puntos críticos. Luego el mínimo se alcanza en uno de los extremos y se comprueba que el menor coste es en x=0, que para mí significaba que bajo tierra no se hacía nada.
Y eso es todo, saludos.
:
:
;)
Hola Alex Mate!
Llamando x a lo que indica el dibujo, la función coste sería:
$$\begin{align}&f(x)=25000 \sqrt{16+x^2}+20000(4-x)\\&\\&Domf(x)=[0,4]\\&Derivando:\\& f'(x)=25000 \frac{1}{2 \sqrt{16+x^2}}2x-20000=\frac{25000x}{\sqrt{16+x^2}}-20000\\&\\&f'(x)=0\\&\frac{25000x}{\sqrt{16+x^2}}-20000=0\\&\\&\frac{25000x}{\sqrt{16+x^2}}=20000\\&\\&5x=4 \sqrt{16+x^2}\\&elevando º al \ cuadrdo:\\&25x^2=16(16+x^2)\\&9x^2=16^2\\&x=\frac{16}{3}=5.3333 \not \in Domf(x)\\&Calculemos \ el \ valor \ en \ los \ extremos \ del \ dominio:\\&f(0)=25000·16+20000·4=180000\\&f(4)=25000 \sqrt{32}=141421.35\\&\end{align}$$el mínimo absoluto esta en x=4, es decir cuando toda la tuberia va sobre el pantano