Desarrollar el siguiente limite cuando "x" tiende a infinito
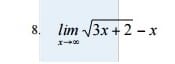
Buenos días amigos de todo expertos les agradezco su ayuda con este limite
Respuesta de Lucas m
1
1 respuesta más de otro experto
Respuesta de Valero Angel Serrano Mercadal
1
