Como hallar el dominio de definición de la siguiente función?
Sea f la función definida por: f(x)=(x-1/x).lm(x)
1) Hallar el dominio de definición de f y calcula lim+inf f(x) y lim 0+ f(x)
2) Hallar las ramas infinitas de la curva en +infinito.
3) Demostrar que f'(x)= ((x^2+1)lm(x)+x^2-1)/x^2
Deducir que f crece en ]1;+inf[y decrece en ]0,1[
4) Dibuja la curva de f.
1 respuesta
·
·
¡Hola Sia!
Supondré que donde has puesto lm querías decir ln, espero sea así.
$$\begin{align}&f(x)=\left(x+\frac 1x \right)ln\,x\\&\\&\text{Para el dominio tengamos en cuenta que el}\\&\text{argumento de los logaritmos debe ser positivo}\\&\text{y con eso basta porque se elimina también el }\\&\text{caso de 0 en el denominador}\\&\\&Dom f=\mathbb R^+ = (0,\;\infty)\\&\\&2)\end{align}$$No entiendo yo lo que quiere decir ramas infinitas en el infinito, podrías ver si dice eso y si lo dice explicarme si se refiere a las asíntotas.
Espero la aclaración.
Saludos.
:
:
Quise decir ln (logaritmo) ,y es así como lo pone, pone ramas infinitas , supongo que son las asíntotas
Es que no puede ser otra cosa. En + infinito el límite es infinito, luego no hay asíntota horizontal. No hay vertical porque las verticales son en puntos x finitos. Luego solo puede haber asíntota oblicua que sería de la forma:
y = mx + b
donde
$$\begin{align}&m=\lim_{x\to\infty}\frac{f(x)}{x}\\&\\&\text{y si }m \in \mathbb R-\{0\}\\&\\&b=\lim_{x\to\infty}(f(x)-mx)\\&\\&m=\lim_{x \to \infty} \frac{\left(x-\frac 1x \right)ln\,x}{x}=\\&\\&\lim_{x \to \infty} \frac{\left(x-\frac 1x \right)ln\,x}{x}=\\&\\&\lim_{x\to\infty}\left(1-\frac{1}{x^2}\right)ln\,x=(1+0)·\infty=\infty\\&\\&\text{Luego tampoco hay asíntota vertical}\\&\\&3)\\&f'(x)=\left(1+\frac 1{x^2}\right)ln\,x+\left(x-\frac 1x \right)\frac 1x=\\&\\&\frac{x^2+1}{x^2}·ln\,x+1-\frac 1{x^2}=\\&\\&\frac{(x^2+1)ln\,x+x^2-1}{x^2}\\&\\&\text{calculamos las raíces}\\&\\&Si\; 0\lt x\lt 1\implies \\&lnx\lt 0;\;\;x^2-1\lt 0\implies f'(x)\lt 0\implies decreciente\\&\\&Si \;x=0\implies f'(x)=ln\,0-1=0\\&\\&Si \;x\gt 1\implies\\&ln\,x\gt 0;\;\;x^2-1\gt 0\implies f'(x)\gt 0 \implies creciente\end{align}$$Y esta es la gráfica:
:
:
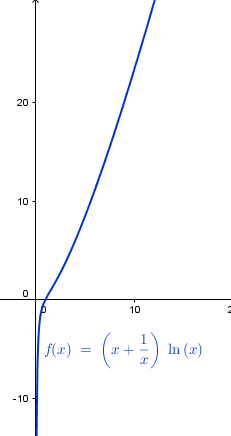
