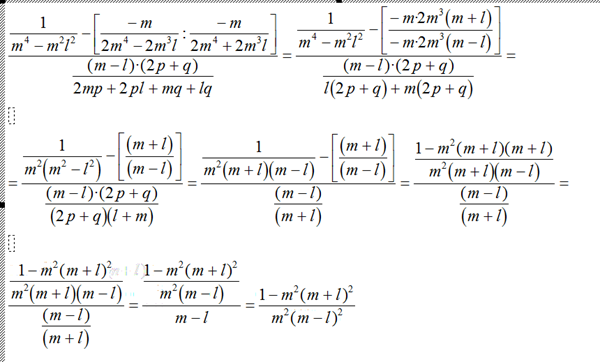Reducir a su mínima expresión el siguiente problema matematico.
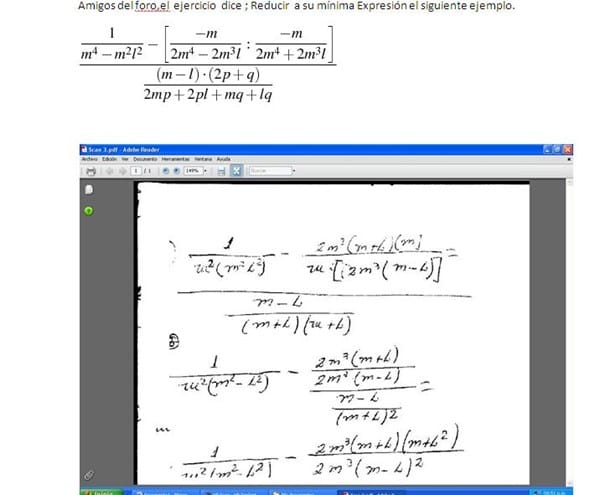
No puedo llegar al resultado exacto y he realizado en forma escrita a mano parte de la solución del mismo. Lo hice para saber si esta bién desarrollado lo que he fáctoreado, ya que cuando llego al final, el resultado no es igual.
Al simplificar completo se llega a : 1 - m^2 ( m + l ) ^2 / m^2 ( m - l ) ^2, necesito saber que estoy haciendo mal para solucionarlo, envío una imagen del ejercicio y lo que hice hasta parar.
3 Respuestas
Respuesta
1
A ver, intentaré hacer en cada paso solo 1 ó 2 operaciones
$$\begin{align}&\frac{\frac{1}{m^4-m^2l^2}-\bigg[\frac{-m}{2m^4-2m^3l}:\frac{-m}{2m^4+2m^3l} \bigg]}{\frac{(m-l)(2p+q)}{2mp+2pl+mq+lq}}=\\&\text{Reacomodo la división y saco factor común en el último denominador}\\&\frac{\frac{1}{m^4-m^2l^2}-\bigg[\frac{-m}{2m^4-2m^3l}\cdot \frac{2m^4+2m^3l}{-m} \bigg]}{\frac{(m-l)(2p+q)}{2p(m+l)+q (m+l)}}=\\&\frac{\frac{1}{m^4-m^2l^2}-\bigg[\frac{2m^4+2m^3l}{2m^4-2m^3l} \bigg]}{\frac{(m-l)(2p+q)}{(m+l)(2p+q)}}=\\&\frac{\frac{1}{m^2(m^2-l^2)}-\bigg[\frac{2m^3(m+l)}{2m^3(m-l)} \bigg]}{\frac{(m-l)}{(m+l)}}=\\&\frac{\frac{1}{m^2(m-l)(m+l)}-\frac{(m+l)}{(m-l)}}{\frac{(m-l)}{(m+l)}}=\\&\frac{\frac{1-(m^2(m+l)^2)}{m^2(m-l)(m+l)}}{\frac{(m-l)}{(m+l)}}=\\&\frac{1-(m^2(m+l)^2)}{m^2(m-l)^2 }=\frac{1-[m(m+l)]^2}{m^2(m-l)^2 }\\&\text{Creo que puede quedar así o desarrollar la diferencia de cuadrados, teniendo}\\&\frac{(1-m(m+l))(1+m(m+l))}{m^2(m-l)^2 }\end{align}$$y no se me ocurre que más simplificar...
Gracias se me despejaron todas las dudas que tenia en la simplificación de este ejercicio.
Saludos!
Respuesta de Lucas m
1
Has aquí se puede simplificar
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Hfarías!
Vas a ahorrar algún paso si te fijas en esto:
$$\begin{align}&\frac ab\div \frac ac= \frac{ac}{ab}=\frac cb\\&\\&\text{con ello avnzaremos mucho en la resolución del corchete}\\&\\&=\frac{\frac{1}{m^4-m^2l^2}-\left[ \frac{-m}{2m^4-2m^3l}\div \frac{-m}{2m^4+2m^3l} \right]}{\frac{(m-l)·(2p+q)}{2mp+2pl+mq+lq}}=\\&\\&\text{No saltaré pasos pero trabajaré todo lo posible en cada uno}\\&\\&\frac{\frac{1}{m^2(m^2-l^2)}-\frac{2m^4+2m^3l}{2m^4-2m^3l}}{\frac{(m-l)·(2p+q)}{2p(m+l)+q(m+l)}}=\\&\\&\frac{\frac{1}{m^2(m+l)(m-l)}-\frac{m+l}{m-l}}{\frac{(m-l)·(2p+q)}{(m+l)+(2p+q)}}=\\&\\&\frac{\frac{1-m^2(m+l)(m+l))}{m^2(m+l)(m-l)}}{\frac{m-l}{m+l}}=\frac{\frac{1-m^2(m+l)(m+l))}{m^2(m-l)}}{m-l}=\\&\\&\frac{1-m^2(m+l)^2}{m^2(m-l)^2}\\&\\&\text{o para hacer dos potencias menos}\\&\\&\frac{1-[m(m+l)]^2}{[m(m-l)]^2}\\&\\&\end{align}$$:
: