Halle del solido generado al rotar sobre el eje por problema con integrales

·

·

¡Hola Oscar!

Al girar sobre el eje x=-1, que es un eje vertical, los límites de integración son valores de la y, luego debemos calcular los valores de y par la intersección de las dos curvas

x=y^2

x=2y

luego

y^2=2y

y^2 - 2y =0

y(y-2) = 0

y los cortes son

y=0

y=2

Debes llevar la recta x=-1 a la recta x=0  que es el eje Y

Para ello hay que sumar 1 en la coordenada x de los puntos de la curva.

Así la curva de puntos

(y^2, y) se transforma en (y^2+1, y) respecto de un sistema de coordenadass que tenga x=-1 como eje Y, luego su ecuación en ese sistema es

x=y^2+1

Y la recta

(2y, y)  se transforma en (2y+1, y)   ==> x=2y+1

De todas formas este ejemplo es bastante más complicado que el anterior será bueno hacer la gráfica. Aunque la perspectiva brilla por su ausencia, debería haber hecho de puntos la curva x=y^2 ya que el sólido la tapa.

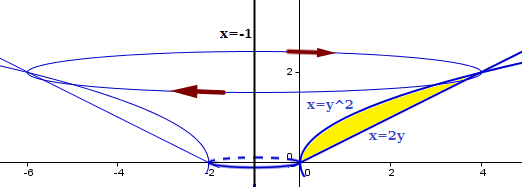
El volumen será el generado por la recta menos el generado por la parábola, se puede calcular en una sola integral.

$$\begin{align}&V=\pi\int_{y_1}^{y_2}(f(y)^2-g(y)^2)dy\\&\\&\\&V=\pi\int_0^2\left((2y+1)^2-(y^2+1)^2\right)dy=\\&\\&\pi \int_0^2(4y^2+4y+1-y^4-2y^2-1)dy=\\&\\&\pi \int_0^2(-y^4+2y^2+4y)dy =\\&\\&\pi\left[-\frac{y^5}{5}+\frac{2y^3}{3}+2y^2  \right]_0^2=\\&\\&\pi\left(-\frac {32}5+\frac {16}3+8\right)= \pi·\frac{-96+80+120}{15}=\\&\\&\frac {104}{15}\pi\approx 21.78170906\, u^3\\&\end{align}$$

:

: