Calcular el área de la región limitada por las curvas

Al despejar x en función de y es como si tuvieramos las funciones inversas.

Las gráficas de dos funciones inversas son simétricas respecto la bisectriz del primer cuadrante. Las originales están en rojo y las inversas en verde.

Observa que la superficie a determinar es la misma.

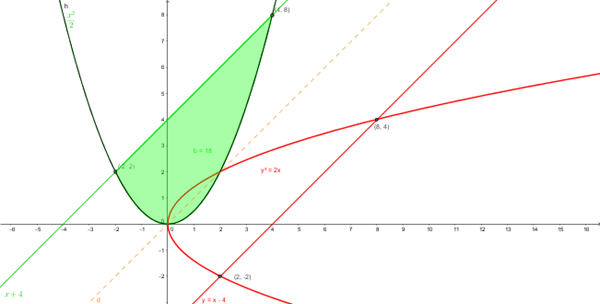
Observa también que si quisieras calcular el área con las funciones iniciales (rojas) tendrías que despejar la y=sqrt(2x) y=-sqrt(2x)

Parábola horizontal son dos funciones. Y para calcular el área tendrías que descomponer el recinto en dos superfícies:

Entre 0 y 2 (comprendida entre las dos funciones radicales) y

Entre 2 y 8 (comprendida entre la radical positiva y la recta).

Al hacer las inversas el área sale con una sola integral entre -2 y 4 de la recta menos la parábola vertical. (En verde).

Si al hacer la inversa no intercanvias las letras de las variables haz la integral con y:

$$\begin{align}&y^2=2x \Rightarrow x=\frac{y^2}{2}\\&\\&y=x-4 \Rightarrow x=y+4\\&\\&\\&Area=\int_{-2}^4(y+4-\frac{y^2}{2})dy=\\&\\&\Bigg[\frac{y^2}{2}+4y-\frac{y^3}{6} \Bigg]_{-2}^4=\\&\\&(8+16-\frac{64}{6})-(2-8-\frac{-8}{6})=18  \  \ u^2\end{align}$$

Saludos

;

;