Resuelve los siguientes problemas de máximos y mínimos, así como su representación gráfica de una función.
Se desea inscribir un cilindro circular recto de volumen máximo dentro de un cono como lo muestra la siguiente figura:
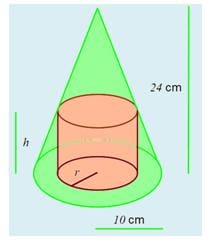
Hallar las dimensiones de dicho cilindro.
2 respuestas más de otros expertos
Sea S el vértice del cono
Sea Q el centro de la circunferencia superior del cilindro
Sea O el centro de la circunferencias de la bases:
Por semejanza de los triangulos SQN y SOA:
$$\begin{align}&\frac{SQ}{SO}=\frac{QN}{OA}\\&\\&\frac{24-h}{24}=\frac{r}{10}\\&\\&r=\frac{5}{12}(24-h)\\&\\&V= \pi r^2h\\&\\&V(h)= \pi·\frac{25}{144}(24-h)^2·h\\&\\&DominioV(h)=(0,24)\\&\\&V'(h)=\frac{ \pi 25}{144}[-2(24-h)h+(24-h)^2]=\\&\\&\frac{ \pi 25}{144}[(24-h)(-2h+24-h)]=\\&\\&\frac{ \pi 25}{144}[(24-h)(24-3h)]\\&\\&V'(h)=0 \Rightarrow 24-3h=0 \Rightarrow h=8\\&\Rightarrow r=\frac{20}{3}\\&\\&V'(7)>0 \ (creciente)\\&V'(9)<0 \ (decreciente)\\&\Rightarrow h=8 \ (Máximo)\\&\\&\end{align}$$
Una pregunta, una compañera mía le dio igual h=8 y r=6.6 pero usando la fórmula del cilindro y derivando, ¿esta bien?
Votar Excelente es lo correcto
Puedes cambiar tu voto
¿No entendiste algo?
$$\begin{align}& \end{align}$$¡Hola Ana!
·
El cono determina dentro un triangulo rectángulo de altura 24cm y radio 10cm.
Sobre la hipotenusa de ese triángulo estará el borde superior del cilindro, ello obliga a que el radio y la altura del cilindro inscrito tengan una relación entre si.
Si colocamos un cilindro inscrito de altura h el triángulo que forma es semejante y tendrá los lados proporcionales
h/24 = base/10
esta base es lo que sobra al cilindro luego el radio del cilindro será
r = 10-base
base = 10-r
por lo tanto la relación entre radio y altura del cilindro es
h/24 = (10-r)/10
despejare h que se ve más facil
h = (24/10)(10-r)
El volumen del cilindro es:
$$\begin{align}&V= \pi·r^2·h=\\&\\&\pi·r^2·\frac{24}{10}(10-r)=\\&\\&24\pi\left(r^2-\frac{r^3}{10}\right)\\&\\&\text{V es una función de r, la derivamos}\\&\text{ e igualamos a 0 para calcular el máximo}\\&\\&V'(r)=24\pi\left(2r-\frac{3r^2}{10}\right)=0\\&\\&2r-\frac{3r^2}{10}=0\\&\\&20r -3r^2=0\\&\\&\text{r=0 no sirve, da volumen 0}\\&\\&20-3r=0\\&\\&r=\frac{20}{3} \;cm= 6.666...\;cm\\&\\&\text{La derivada segunda es}\\&\\&V''(r)=24\pi\left(2-\frac{6r}{10} \right)\\&\\&V''\left(\frac {20}3\right)=24\pi\left(2-\frac{40}{10} \right)=-48\pi\\&\\&\text{Luego es un máximo}\\&\\&\text{Y la altura será}\\&\\&h=\frac{24}{10}\left(10-\frac {20}3 \right)=\frac {12}{5}·\frac{10}{3}=8cm\\&\end{align}$$Luego esas son las dimensiones del cilindro:
Radio = 6.6666... cm
Altura = 8 cm
·
Y eso es todo.