Aplicaciones de la derivada 3
Hallar las dimensiones de un cono recto circular de volumen mínimo que pueda inscribirse una esfera de 8 plg de diámetro.
1 respuesta
Creo que el enunciado está mal. El cono puede hacerse con base muy pequeña, de modo que el límite del volumen sería cero cuando fuese prácticamente una linea. Luego creo que la pregunta debe ser:
Hallar las dimensiones de un cono recto circular de volumen máximo que pueda inscribirse una esfera de 8 plg de diámetro.
El enunciado esta correcto, pero ya ves que en algunas ocasiones ha estado mal, si es posible desarrollalo como tu dices.
Nada, tal como está el cono de volumen mínimo sería una de altura 8 y radio 0 que ni siquiera se puede llamar cono.
Vamos a hacer el de volumen máximo.
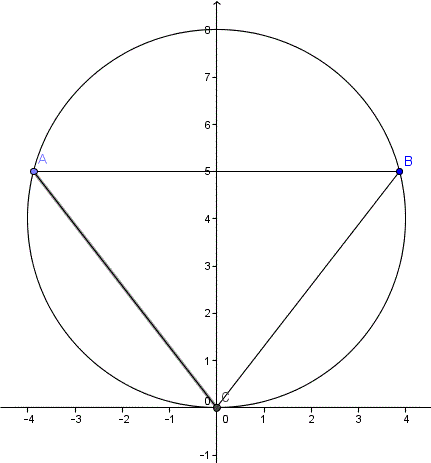
Tal como está la imagen del corte con un plano de la figura, la ecuación de la circunferencia es
x^2 + (y-4)^2 = 16
Si le damos una altura h a la base del cono que está hacia arriba el punto de intersección entre el triángulo y la circunferencia son los puntos A y B.
x^2 + (h-4)^2 = 16
x^2 = 16 - (h-4)^2
x = sqrt[16 - (h-4)^2]
Esto será el radio del cono.
Entonces el volumen es
V = (1/3)Pi·h·r^2 =
(1/3)Pi·h·[16-(h-4)^2] =
(1/3)Pi·h·(16 - h^2 + 8h -16) =
(1/3)Pi(8h^2-h^3)
Derivamos respecto a h e igualamos a 0 para obtener el máximo
(1/3)Pi(16h-3h^2) = 0
h(16-3h) = 0
h=0 es un mínimo
16-3h = 0
h = 16/3 = 5.3333... pulgadas
Y ahora calculamos el radio
r = sqrt[16 - (h-4)^2] =
sqrt[16 - (16/3-4)^2] =
sqrt[16 - (4/3)^2] =
sqrt(16 - 16/9) =
sqrt[(144-16)/9] =
sqt(128/9) = 8 sqrt(2) / 3 = 3.771236166 pulgadas
Luego las dimensiones son
h = 16/3 ''
r = 8·sqrt(2)/3
Y eso es todo.
