Ecuaciones diferenciales, me ayuda por favor a resolver la siguiente ecuación

Entiendo que la pregunta no es resolver la ecuación, lo cual podría ser muy complicado, sino comprobar que la respuesta es verdadera usando algún SAC.

Yo voy a usar Maxima que es en que me manejo un poco.

Pero antes de seguir voy a ver como es la solución, que no ha salido en LaTeX sin efectuarse

$$\begin{align}&y=20 \frac{\cos(5 Inx)}{x}+3\frac{sen(Inx)}{x}\end{align}$$

veo que has usado la letra i mayúscula en lugar de la l minúscula, es algo muy frecuente con las muchas fuentes que no distinguen esos dos caracteres, es la ele porque sonlas iniciales de logaritmo neperiano o logaritmo natural.

$$\begin{align}&y=20 \frac{\cos(5 lnx)}{x}+3\frac{sen(lnx)}{x}\end{align}$$

De todas formas no vas a usar ln sino log, los anglosajones usan log para referirse al logaritmo neperiano y en casi todos los pregramas deberás usarlo.

Lo primero definiremos la función, aquí hay que tener cuidado de escribirla bien ya que el ordenador no tiene la consideración de un maestro. Además, por estar usando Máxima, no podemos dejarnos ni un solo signo de multiplicar, en todo sitio donde haya una multiplicación debe aparecer un asterisco, en todo.

Y luego evaluaremos la expresión, teniendo en cuenta que la forma de escribir la derivada enésima de una función f(x) respecto de x es

diff(f(x),x,n)

Y otra función interesante es radcan

Radcan(expresion)

Simplifica una expresión

Radcan(%)

Simplifica la última respuesta que ha salido.

Luego tendremos que escribir estas dos líneas y pulsar CTRL+ENTER

Y lo que hay que escribir es

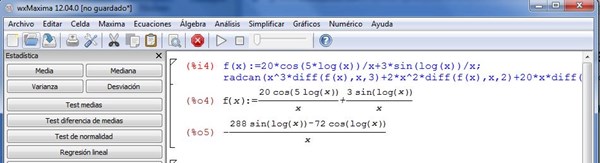
f(x):=20*cos(5*log(x))/x+3*sin(log(x))/x;
radcan(x^3*diff(f(x),x,3)+2*x^2*diff(f(x),x,2)+20*x*diff(f(x),x)-78*f(x));

Yel resultado que da es:

-(288*sin(log(x))-72*cos(log(x)))/x

Escrito en LaTeX y españolizado sería

$$\begin{align}&-\frac{288sen(lnx)-72cos(lnx)}{x}\end{align}$$

Pues lo que dice el enunciado es falso.  Revisa a ver si está bien el enunciado y si yo lo he interpretado bien.

El enunciado es correcto, muchas gracias.

Me puede decir como obtener el programa que utilizo (wxMaxima) ya que me interesa aprender a manejar el programa o lo puedo descargar gratis.

También me gustaría saber si puedo utilizar algún otro programa para resolver este tipo de ejercicios.

Mil gracias por su ayuda.

PD. Tengo una duda ¿por que me llegan correos a mi nombre con preguntas que yo no eh solicitado?