Cálculo de superficie entre dos círcunferencias secantes

Hagamos la figura.

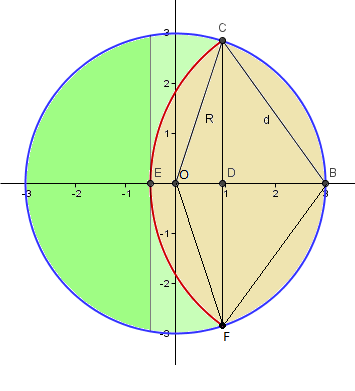
La parte que se come es la marrón. Se puede obtener cono la suma del segmento circular CBF de la circunferencia de radio R mas la del segmento circular CEF de la circunferencia de radio D.

Para calcular el área de esos sectores circulares deberemos conocer los ángulos COF y CBF y las distancias OD, CD y DB.

Y el área de los segmentos es la de los sectores menos la de los triángulos COF y CBF

Es decir, el área marrón es

Área(sector COF) - Área(triángulo COF) + Área(sector CBF) - Área(triangulo CBF) =

Área(sector COF) + Área(sector CBF) - OD·CD - DB·CD =

Área(sector COF) + Área(sector CBF) - CD(OD+DB) =

Área(sector COF) + Área(sector CBF) - CD · R

Y para calcular los ángulos habrá que usar trigonometría. Tomamos los triángulos rectángulos OCD y BCD. Por el teorema de Pitágoras tendremos:

$$\begin{align}&\overline{CD}^{\;2}=R^2-\overline{OD}^{\;2}\\ &\\ &\overline{CD}^{\;2}=d^2-\overline{DB}^{\;2}=d^2-(R-\overline{OD})^{2}\\ &\\ &R^2-\overline{OD}^{\;2}=d^2-\overline{DB}^{\;2}=d^2-(R-\overline{OD})^{2}\\ &\\ &R^2-\overline{OD}^{\;2}=d^2-R^2+2R·\overline{OD}-\overline{OD}^{\;2}\\ &\\ &R^2=d^2-R^2+2R·\overline{OD}\\ &\\ &2R·\overline{OD}=2R^2-d^2\\ &\\ &\overline{OD}=\frac{2R^2-d^2}{2R}\\ &\\ &\overline{CD}=\sqrt{R^2-\left(\frac{2R^2-d^2}{2R}  \right)^2}=\\ &\\ &\sqrt{R^2-\frac{4R^4-4R^2d^2-d^4}{4R^2}}=\\ &\\ &\sqrt{\frac{4R^4-4R^4+4R^2d^2+d^4}{4R^2}}=\\ &\\ &\frac{\sqrt{4R^2d^2+d^4}}{2R}\end{align}$$

Y los ángulos son

$$\begin{align}&\widehat{COF} =2arcos \frac{\overline{OD}}{R}=\\ &\\ &2arccos \frac{\frac{2R^2-d^2}{2R}}{R}=\\ &\\ &2arcos \frac{2R^2-d^2}{2R^2}\\ &\\ &2arcos \left(1-\frac{d^2}{2R^2}\right)\\ &\\ &\\ &\\ &\widehat{CBF}= 2arcos \frac{R-\overline{OD}}{d}=\\ &\\ &2arccos \frac{R-\frac{2R^2-d^2}{2R}}{d}=\\ &\\ &2arcos \frac{2R^2-2R^2+d^2}{2Rd}=\\ &\\ &2arcos \frac{d^2}{2Rd} =\\ &\\ &2arcos \frac d{2R}\end{align}$$

El área de cada sector es su respectivo radio al cuadrado por la mitad del ángulo medido en radianes. Recuerda que de una circunferencia con ángulo 2Pi radianes tenemos un círculo con área Pi·R^2. Con todos los elementos calculados se forma esta ecuación

$$R^2·arcos \left(1-\frac{d^2}{2R^2}\right)+d^2·arcos \frac{d}{2R}-\frac{\sqrt{4R^2d^2+d^4}}{2R}·R= \pi \frac{R^2}{2}\\ \\ \text{Como }\cos(a+b)=cosa·cosb-sena·senb\\ \\ R^2\left[arcos  \right]$$

Nada, que por aquí no se llega a ningún lado, quien sepa despejar d en esa ecuación merece mi más alto reconocimiento.

Espera, unas horas porque ahora tengo que dejar el ordenador. Lo intentaré resolver por integrales, que es lo primero que intenté, pero como no eran sencillas pensé que a lo mejor se podía hacer más fácil así y ahora veo que no.

De todas forma podrías decirme qué estudias y por qué método se supone que hay que solucionarlo. Ya te digo que lo voy a intentar por integrales, si fuera por algún método geométrico lo desconozco y lo único que podría hacer es si me mandases el libro de la teoría.

Espera unas horas como te decía o contesta lo que te preguntaba, pero no cierres la pregunta.

Para que lo verde sea la mitad debe cumplirse que el área marrón entre E y O sea igual a la verde entre O y D

El punto E es

E=(r-d, 0)

El punto D estaba calculado, es

D = ((2R^2-d^2)/(2R) , 0)

La circunferencia de hierba tiene ecuación

x^2+y^2=R^2

y = sqrt(R^2-x^2)

La que hace la cabra tiene ecuación

(x-R)^2+y^2 = d^2

y= sqrt[d^2-(x-R)^2]

$$\begin{align}&\int_{R-d}^0 \sqrt{d^2-(x-R)^2}dx=\int_0^{\frac{2R^2-d^2}{2R}}\left(\sqrt{R^2-x^2}-\sqrt{d^2-(x-R)^2}\right)dx\\ &\\ &\text{Separando la derecha en dos, pasando la segunda a la izquierda}\\ &\text{y juntándola con la que hay queda}\\ &\\ &\int_{R-d}^{\frac{2R^2-d^2}{2R}} \sqrt{d^2-(x-R)^2}dx=\int_0^{\frac{2R^2-d^2}{2R}}\sqrt{R^2-x^2}dx\\ &\\ &\end{align}$$

No es que no sepa hacerlas, pero aparte de ser lioso, creo que va a dar una respuesta tan mala como con el método anterior. Por eso, antes de perder mucho tiempo la resolveré con el ordenador para ver si merece la pena el esfuerzo.

Las integrales quedan:

$$\begin{align}&-\frac{d^3 \sqrt{4R^2-d^2}+R^2\left(4d^2 arcsen \frac{d}{2R}-2\pi d^2\right)}{8R^2}=\\ &\\ &\frac{4R^4 arcsen \frac{2R^2-d^2}{2R^2}+(2R^2d-d^3)\sqrt{4R^2-d^2}}{8R^2}\\ &\\ &/-------/\\ &\\ &-R^2\left(4d^2 arcsen \frac{d}{2R}-2\pi d^2\right)=\\ &\\ &4R^4 arcsen \frac{2R^2-d^2}{2R^2}+2R^2d \sqrt{4R^2-d^2}\\ &\\ &/-------/\\ &\\ &\\ &-R^2\left(4d^2 arcsen \frac{d}{2R}-2\pi d^2\right)=\\ &\\ &4R^4 arcsen \frac{2R^2-d^2}{2R^2}+2R^2d \sqrt{4R^2-d^2}\\ &\\ &/-------/\\ &\\ &-4d^2 arcsen \frac{d}{2R}+2\pi d^2=4R^2 arcsen \frac{2R^2-d^2}{2R^2}+2d \sqrt{4R^2-d^2}\\ &\\ &2R^2· arcsen\left(1-\frac{d^2}{2R^2}  \right)+2d^2arcsen \frac{d}{2R}+d(\sqrt{4R^2-d^2}-\pi d)=0\end{align}$$

Como suponía, queda una ecuación equivalente a la que calculé de la otra forma.

Pues esto solo se puede resolver numéricamente pienso yo. Dime si estás estudiando eso. Podemos resolverlo por el método de dividir en intervalos por la mitad o por el método de Newton que es más exacto y rápido pero más complicado.

Dime cómo lo necesitas.

Lo primero para resolver esa ecuación numéricamente es que no puede haber dos incógnitas R y d. A todos se nos ocurre que la proporción entre ambas es fija, luego vamos a hacer que todo dependa de una variable x = d/R. Para que la ecuación tome esa forma dividimos entre R^2

$$\begin{align}&2R^2· arcsen\left(1-\frac{d^2}{2R^2}  \right)+2d^2arcsen \frac{d}{2R}+d(\sqrt{4R^2-d^2}-\pi d)=0\\ &\\ &2 \frac{R^2}{d^2}arcsen\left(1-\frac{d^2}{2R^2}  \right)+2arcsen \frac{d}{2R}+\frac{\sqrt{4R^2-d^2}-\pi d}{d}=0\\ &\\ &\frac{2}{x^2} arcsen\left(1-\frac{x^2}{2}\right)+2arcsen \frac x2+\sqrt{\frac{4R^2-d^2}{d^2}}-\pi=0\\ &\\ &\frac{2}{x^2} arcsen\left(1-\frac{x^2}{2}\right)+2arcsen \frac x2+\sqrt{\frac{4}{x^2}-1}-\pi=0\\ &\\ &\text{Multiplicamos por } x^2 \text{ para que queden derivadas más fáciles}\\ &\\ &2arcsen\left(1-\frac{x^2}{2}\right)+2x^2arcsen \frac x2+\sqrt{4x^2-x^4}-\pi x^2=0\\ &\end{align}$$

El método de Newton-Raphson es

$$\begin{align}&x_{n+1}=x_n-\frac{f(x)}{f'(x)}\\ &\\ &x_{n+1}=x_n- \frac{2arcsen\left(1-\frac{x^2}{2}\right)+2x^2arcsen \frac x2+\sqrt{4x^2-x^4}-\pi x^2}{\frac{-4}{\sqrt{4-x^2}}+4x\,arcsen \frac x2+\frac{2x^2}{\sqrt{4-x^2}}+\frac{4-2x^2}{\sqrt{4-x^2}}-2\pi x}\\ &\\ &\\ &x_{n+1}=x_n- \frac{2arcsen\left(1-\frac{x^2}{2}\right)+2x^2arcsen \frac x2+\sqrt{4x^2-x^4}-\pi x^2}{4x\,arcsen \frac x2-2\pi x}\\ &\\ &\text {comenzamos con }x_0=1\\ &\\ &x_1 = 1.163496672\\ &\\ &x_2 = 1.158730912\\ &\\ &x_3 = 1.158728473\\ &\\ &x_4=1.158728473\\ &\\ &x_5=1.158728473\end{align}$$

He dejado que saliese tres veces la misma respuesta por si los decimales internos de la calculadora aun podían hacer variar la respuesta. Pero no, la respuesta es esta:

La cuerda que se debe dar a la cabra es 1.158728473 veces el radio del círculo de hierba.

me habían dado otra respuesta con un resultado diferente. que opinas?

Se trata de una ecuación trascendente,
resoluble por métodos gráficos ó numéricos
El´área de la mitad de la superficie buscada
es un segmento circular
con un ángulo de arco 2 ?1 y radio R1 es
Suponemos la incógnita el radio R1 que es la longitud de la soga
y R2 el radio del círculo de hierba.
Aseg1 = (1/2) R1^2 ( 2 ?1 - sen(2 ?1))
Para el otro segmento
Aseg2 = (1/2) R2^2 ( 2 ?2 - sen(2 ?2))
En total
Atot = Aseg1 + seg2 = (1/2) R1^2 ( 2 ?1 - sen(2 ?1)) + (1/2) R2^2 ( 2 ?2 - sen(2 ?2))
Buscamos que
Atot = 1/2 (p R2^2)
queda
a) (1/2) R1^2 ( 2 ?1 - sen(2 ?1)) + (1/2) R2^2 ( 2 ?2 - sen(2 ?2)) = 1/2 (p R2^2)
ó
a) (R1/R2)^2 ( 2 ?1 - sen(2 ?1)) + ( 2 ?2 - sen(2 ?2)) = p
**************************************…
Se debe cumplir
por igualdad de cuerdas circulares
b) R1 sen(?1) = R2 sen(?2)
ó
b) (R1/R2) = sen(?2)/sen(?1)
Además , la distancia entre centros es R2
porque la soga está atada en el borde del círculo de radio R2
R1 cos(?1) + R2 cos(?2) = R2
R1 cos(?1) = R2 (1 - cos(?2))
ó
c) R1/R2 = (1 - cos(?2))/cos(?1)
======================================
de b) y c)
sen(?2)/sen(?1) = (1 - cos(?2)) / cos(?1)
sen(?2) cos(?1) = sen(?1) - sen(?1) cos(?2)
sen(?2) cos(?1) + cos(?2) cos(?1) = sen(?1)
sen(?2 + ?1) = cos(?1)
Descartamos ?2 = 0
?2 + ?1 + ?1 = p
?2 = p - 2 ?1
Esto es fácil de verificar directamente,
dada la relación de ángulos semiinscriptos y centrales.
Remplazamos en b)
d) (R1/R2) = sen(?2)/sen(?1)
d) (R1/R2) = sen(2 ?1)/sen(?1)
d) (R1/R2) = 2 cos(?1)
--------------------------------------…
En total, tenemos el sistema trascendente con 3 incógnitas
R1/R2 ; ?1 ; ?2
a) (R1/R2)^2 ( 2 ?1 - sen(2 ?1)) + ( 2 ?2 - sen(2 ?2)) = p
b) (R1/R2) = sen(?2)/sen(?1)
c) (R1/R2) = (1 - cos(?2))/cos(?1)
**************************************…
Avancemos un poco más
Remplazamos en a)
e) (R1/R2)^2 ( 2 ?1 - sen(2 ?1)) + ( 2(p - 2 ?1) - sen(2(p - 2 ?1))) = p
e) (R1/R2)^2 ( 2 ?1 - sen(2 ?1)) + ( 2p - 4 ?1) + sen(4 ?1) = p
e) (R1/R2)^2 ( 2 ?1 - sen(2 ?1)) = p - ( 2p - 4 ?1) - sen(4 ?1)
e) (R1/R2)^2 ( 2 ?1 - sen(2 ?1)) = 4 ?1 - sen(4 ?1) - p
finalmente
e) (R1/R2)^2 = (4 ?1 - sen(4 ?1) - p)/( 2 ?1 - sen(2 ?1))
Como
d) (R1/R2) = 2 cos(?1)
LLegamos a
f) (4 ?1 - sen(4 ?1) - p)/( 2 ?1 - sen(2 ?1)) = 4 cos^2(?1)
f) (4 ?1 - sen(4 ?1) - p) = ( 2 ?1 - sen(2 ?1)) 4 cos^2(?1)
f) 4 ?1 - sen(4 ?1) - p = 8 ?1 cos^2(?1) - 4 sen(2 ?1) cos^2(?1)
f) 4 ?1 - 8 ?1 cos^2(?1) - p = sen(4 ?1) - 4 sen(2 ?1) cos^2(?1)
f) 4 ?1 - 8 ?1 cos^2(?1) - p = 2 sen(2 ?1) cos(2 ?1) - 4 sen(2 ?1) (1/2) (1 + cos(2?1) )
f) 4 ?1 ( 1- 2 cos^2(?1)) - p = 2 sen(2 ?1) cos(2 ?1) - 2 sen(2 ?1) - 2 sen(2 ?1) cos(2?1)
f) 4 ?1 ( 1- 2 cos^2(?1)) - p = - 2 sen(2 ?1)
f) 4 ?1 = (p - 2 sen(2 ?1)) / ( 1- 2 cos^2(?1))
====================================
Toda esta ecuación trascendente resulta en
?1 = 0.9528
R1/R2 = raíz(2 cos(?1))
R1/R2 = 1.0763
==============
Por ejemplo, para un círculo de 10 m de hierba
con un cuerda de 10.76 m se tiene un área de pastura
de la mitad del área de hierba

Has debido usar caracteres que no se pueden ver en esta página, por eso aparecen muchas interrogaciones y no se puede ver el razonamiento.

Yo me fio completamente de mi respuesta. Lo único que puedo hacer es que veas las gráficas de ambos y veras que la mía es la buena.

Esta es la gráfica con mi respuesta:

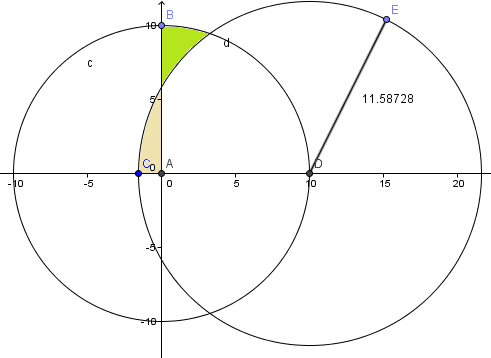
Puedes ver como se intuye que lo que no se come de la semicircunferencia en verde se compensa lo que se come de la otra en marrón.

Y esta es la gráfica con la respuesta que te han dado.

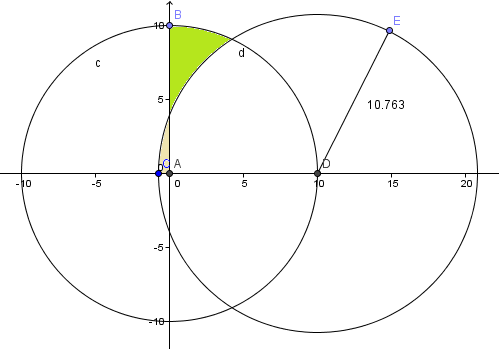
Creo que sobran los comentarios, la cabra se habrá quedado con hambre.

Y eso es todo, no puedo analizar la respuesta que te han dado por eso que te decía que no se ven muchos caracteres, pero algo está mal en lo que han hecho.

Si lo que te asusta es que haya usado integrales que no he resuelto directamente, no te preocupes. Voy a resolver numéricamente la ecuación trascendente que me dio en el primer intento donde no se usaban integrales, que tiene que dar la misma respuesta, espera un poco.

Casi me vuelvo loco porque no salía ni a tiros . En la parte primera tuve un fallo aquí

$$\begin{align}&overline{CD}=\sqrt{R^2-\left(\frac{2R^2-d^2}{2R}  \right)^2}=\\ &\\ &\\ &\sqrt{R^2-\frac{4R^4-4R^2d^2-d^4}{4R^2}}\\ &\\ &\text{en realidad es}\\ &\\ &\sqrt{R^2-\frac{4R^4-4R^2d^2+d^4}{4R^2}}=\\ &\\ &\\ &\sqrt{\frac{4R^4 - 4R^4+4R^2d^2-d^4}{4R^2}}=\\ &\\ &\\ &\sqrt{\frac{4R^2d^2-d^4}{4R^2}}\\ &\\ &\\ &\end{align}$$

Con lo cual la ecuación primera pasa a ser esta.

$$\begin{align}&R^2·arcos \left(1-\frac{d^2}{2R^2}\right)+d^2·arcos \frac{d}{2R}-\frac{\sqrt{4R^2d^2-d^4}}{2R}·R= \pi \frac{R^2}{2}\\ &\\ &\\ &R^2·arcos \left(1-\frac{d^2}{2R^2}\right)+d^2·arcos \frac{d}{2R}-\frac{d\sqrt{4R^2-d^2}}{2}= \pi \frac{R^2}{2}\\ &\\ &\\ &2R^2·arcos \left(1-\frac{d^2}{2R^2}\right)+2d^2·arcos \frac{d}{2R}-d\sqrt{4R^2-d^2}= \pi R^2\\ &\\ &2R^2·arcos \left(1-\frac{d^2}{2R^2}\right)+2d^2·arcos \frac{d}{2R}-d\sqrt{4R^2-d^2}-\pi R^2=0\\ &\\ &\text{dividimos entre }d^2\\ &\\ &2 \frac{R^2}{d^2}·arcos \left(1-\frac{d^2}{2R^2}\right)+2·arcos \frac{d}{2R}-\frac{\sqrt{4R^2-d^2}}{d}-\pi \frac{R^2}{d^2}=0\\ &\\ &\\ &2 \frac{R^2}{d^2}·arcos \left(1-\frac{d^2}{2R^2}\right)+2·arcos \frac{d}{2R}-\sqrt{\frac{4R^2}{d^2}-1}-\pi \frac{R^2}{d^2}=0\\ &\\ &\text {llamamos }x=\frac{d}{R}\\ &\\ &\frac{2}{x^2}·arcos \left(1-\frac{x^2}{2}\right)+2·arcos \frac{x}{2}-\sqrt{\frac{4}{x^2}-1}-\frac{\pi}{x^2}=0\\ &\\ &\text{Multiplicamos por } x^2 \text{ para que salgan derivadas más fáciles}\\ &\\ &2·arcos \left(1-\frac{x^2}{2}\right)+2x^2arcos \frac{x}{2}-\sqrt{4x^2-x^4}-\pi=0\\ &\\ &\end{align}$$

Y ahora resolvemos con el método de Newton-Raphson.

$$\begin{align}&x_{n+1}=x_n-\frac{f(x)}{f'(x)}\\ &\\ &\\ &x_{n+1}=x_n-\frac{2·arcos \left(1-\frac{x^2}{2}\right)+2x^2arcos \frac{x}{2}-\sqrt{4x^2-x^4}-\pi}{\frac{4}{\sqrt{4-x^2}}+4arcos \frac x2-\frac{4x}{\sqrt{4-x^2}}+\frac{2x^2-4}{\sqrt{4-x^2}}}\\ &\\ &\\ &x_{n+1}=x_n-\frac{2·arcos \left(1-\frac{x^2}{2}\right)+2x^2arcos \frac{x}{2}-\sqrt{4x^2-x^4}-\pi}{4arcos \frac x2+\frac{2x^2-4x}{\sqrt{4-x^2}}}\\ &\\ &x_0=1\\ &\\ &x_1= 1.225719518\\ &\\ &x_2= 1.103876838\\ &\\ &x_3 = 1.191116418\\ &\\ &x_4 = 1.134437244\\ &\\ &x^5 = 1.174378514\\ &\\ &x^6 = 1.147492874\\ &\\ &x^7 = 1.166232873\\ &\\ &x^8 = 1.15345602\\ &\\ &x^9 = 1.162307677\\ &\\ &x_{10}= 1.156240041\\ &\\ &x_{11}= 1.160430526\\ &\\ &x_{12}= 1.157551072\\ &\\ &x_{13}= 1.159536655\\ &\\ &x_{14}= 1.158170752\\ &\\ &x_{15} = 1.159111939\\ &\\ &x_{16} = 1.158464148\\ &\\ &x_{17} = 1.158910356\\ &\\ &x_{18} = 1.158603168\\ &\\ &x_{19} = 1.158814728\\ &\\ &x_{20} = 1.158669065\\ &\\ &x_{21}= 1.158769375\\ &\\ &x_{22} = 1.158700305\\ &\\ &x_{23} = 1.158747868\\ &\\ &x_{24} = 1.158715117\\ &\\ &x_{25}= 1.158737669\\ &\\ &x_{26}= 1.15872214\\ &\\ &x_{27}= 1.158732834\\ &\\ &x_{28}= 1.15872547\\ &\\ &x_{29}=1.158730541\\ &\\ &x_{29}= 1.158727049\\ &\\ &x_{30}=1.158729453\\ &\\ &x_{31}= 1.158727798\\ &\\ &x_{32}= 1.158728938\\ &\\ &x_{33}=1.158728153\\ &\\ &x_{34}=1.158728693\\ &\\ &x_{35}= 1.158728321\\ &\\ &x_{36}= 1.158728578\\ &\\ &x_{37}= 1.158728401\\ &\\ &x_{38}=1.158728523\\ &\\ &x_{39}=1.158728439\\ &\\ &x_{40}=1.158728497\end{align}$$

¡Uff! Ya me cansé. Ni tanto ni tal calvo, con la ecuación de los arcosenos salió en tres iteraciones que es demasiado rápido pero con esta no se termina en la vida. Hay algunas ecuaciones a las que este método no les va muy bien. Pero se ve que tiende a la respuesta que dimos antes.

1.158728473

Y eso es todo.

Espera que ya me extrañaba mucho a mí que no convergiera rápidamente, es que me equivoque en la derivada del método de Newton

$$\begin{align}&x_{n+1}=x_n-\frac{f(x)}{f'(x)}\\ &\\ &\\ &x_{n+1}=x_n-\frac{2·arcos \left(1-\frac{x^2}{2}\right)+2x^2arcos \frac{x}{2}-\sqrt{4x^2-x^4}-\pi}{\frac{4}{\sqrt{4-x^2}}+4x·arcos \frac x2-\frac{2x^2}{\sqrt{4-x^2}}+\frac{2x^2-4}{\sqrt{4-x^2}}}\\ &\\ &\\ &x_{n+1}=x_n-\frac{2·arcos \left(1-\frac{x^2}{2}\right)+2x^2arcos \frac{x}{2}-\sqrt{4x^2-x^4}-\pi}{4x·arcos \frac x2}\\ &\\ &x_0=1\\ &\\ &x_1= 1.163496672\\ &\\ &x_2= 1.158730912\\ &\\ &x_3= 1.158728473\\ &\\ &x_4= 1.158728473\end{align}$$

Y ahora se obtiene el mismo resultado e igual de rápido. Que es lo lógico ya que ambas funciones son simétricas respecto del eje X.

Y eso es todo, yo creo que ahora si esta hecho ya todo y bien.