Lo difícil de esto es obtener la integral, una vez la tienes es aplicar los métodos conocidos. Podrán tener algún truco para hacerlas más fácilmente pero no te pondrán algo complicado. Para esto lo mejor es hacer unos cuantos dibujitos. Lo mejor quizás es viendo planos y luego al final hacer algo en 3d. Pueden ser super básicos, lo importante es ver cual es el volumen que te pide
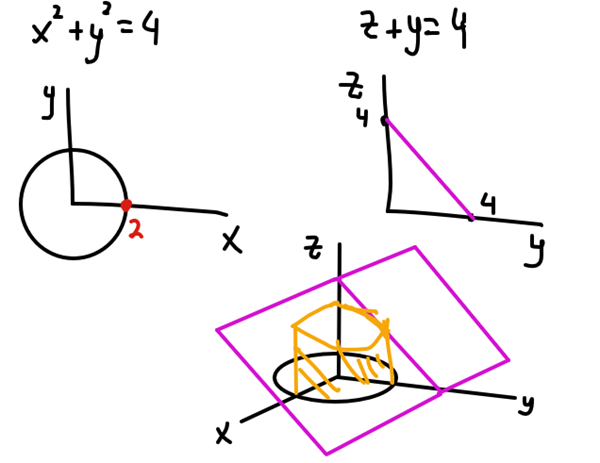
La primera gráfica si la ves desde arriba lo que ves es un circulo de radio 2. Como no depende de z. si haces z=0, 1,2,3,... vas a tener siempre la misma gráfica x^2+y^2=4. Por tanto forma un cilindro. La segunda gráfica por su parte no depende de x, por lo que va a suceder algo similar. Y como depende linealmente de Y y Z, lo que se genera es un plano que lo vemos en morado(o el color que sea...). El volumen por tanto es ese que ves en amarillo. Es un cilindro que tiene un corte diagonal. La integral es
$$\begin{align}&\iiint_V f(x,y) dx \,dy\, dz = \iint_\Omega\left[\int1 dz\right] dx\, dy\end{align}$$f(x,y) = 1 porque quieres calcular el volumen de esa figura que por definicion es calcular la integral triple de 1 (si ya manejas los conceptos mas puedes escribirlo directamente como una integral doble pero lo estoy haciendo por pasos)
Lo mejor es hacer un cambio de coordenadas a cilíndricas debido a ese circulo que tienes en tu eje x-y. Voy a mostrarte las dos integrales pero la cilíndricas es la que sera más fácil de resolver. En el caso de que usemos coordenadas cartesianas, se hace siempre los mismos pasos. Los limites de integración son de abajo hasta arriba, abajo empezamos siempre en z=0, y arriba estamos limitado por el pano z = 4-y.
Ahora pasamos a ver los limites de x e y. Nos concentramos en el plano x-y que contiene el circulo que dibuje arriba. Tienes dos formas de proceder aquí. O haces un barrido horizontal, esto es, recuerda que cuando integras estas sumando unos rectángulos, un prisma rectangular etc. Si haces los rectángulos horizontales que rellenen el circulo. Y va de 0 a 2(el radio), pero la altura de los rectángulos depende de la circunferencia, por tanto X iría de 0 (inicio del rectángulo) hasta X = sqrt(4-y^2). De forma similar si haces los rectangulos verticales, pero ahora la altura de los rectangulos varian segun Y. La otra forma es usar coordenadas cilindricas que debido al circulo tienes que hacer x=r*costheta, y = r*sin(theta). Y en este caso r y theta son independientes. Eso si, hay que añadir a la integral una r debido al cambio de coordenadas (dado por el jacobiano de la transformación si te interesa)
$$\begin{align}& \iint_\Omega\left[\int1 dz\right] dx\, dy = \int_0^2 \int_0^\sqrt{4-y^2} \int_0^{4-y}1 \,dz \,dx\,dy = \int_0^2 \int_0^\sqrt{4-x^2}\int_0^{4-y}1 \,dz \,dy\,dx = \int_0^2\int_0^\frac{\pi}{2}\int_0^{4-2\cdot\sin(\theta)} r\, dz \, d\theta\, dr = 4\pi - \frac{8}{3}\end{align}$$


