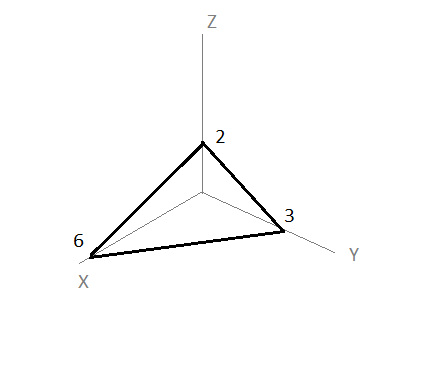Quiero hacer un jacobiano en la siguiente integral pero no se como construir el limite en z
halle el limite de x
0<x/6<1
x/6<y/3<1-x/6
x/6<x/6<y/3+x/6<1
llamando a x/6 =u y x/6+y/3=v pero, mi problema esta en el limite de z me confunde allí
1 respuesta
Como siempre un boceto para aquella figura
- Es fácil ver que
$$\begin{align}&0\leq x \leq 6\end{align}$$
- y que la región triangular en XY es representado por el siguiente conjunto
$$\begin{align}&S_{xy}=\{(x,y):0\leq x\leq 6~,~0\leq x+2y\leq 6\}\end{align}$$- y por ende todo el sólido viene representado por
$$\begin{align}&S=\{(x,y,z):0\leq x\leq 6~,~x\leq x+2y\leq 6~,~x+2y\leq x+2y+3z\leq 6\}\\&\\&\text{Podemos hacer el siguiente cambio de variable: }\\&\\&u=x\\&v=x+2y\\&w=x+2y+3z\\&\\&\text{Despejando: }x= u~.~y=\frac{v-u}{2}~,~ z=\dfrac{w-v}{3}\\&\\&\text{El jacobiano es: }J(u,v,w)=\frac{1}{6}\\&\\&I=\iiint\limits_{S}x~dV=\int_{0}^{6}\int_{u}^{6}\int_{v}^{6} u \cdot \frac{1}{6} ~dw~dv~du\\&\\&I=9\end{align}$$
Errata, me confundí
$$\begin{align}&S_{xy}=\{(x,y):0\leq x\leq 6~,~x\leq x+2y\leq 6\}\end{align}$$
Te lo agradezco mucho, pero una pregunta ¿de que libro aprendiste a hacer jacobiano en i.triples?, porque la mayoría de los libros trae cambio con jacobiano en integrales dobles
Para esta cuestión de integrales múltiples solo leí el libro de L.D. Kudriavtsev, Curso de análisis matemático vol. 2. Es un libro para los que estudian matemática pura, no es difícil de entenderlo pero tampoco es tan sencillo.
Si la mayoría de libros trae solo integrales dobles, es porque se puede expandir de forma análoga a las integralen n-tuples, ya que este tipo de integrales tiene como base la geometría euclideana n-dimensional.
Como consejo puedo decir que despues de hacer el cambio de variable, calcules la integral doble o triple sin la función dentro de la integral, tal integral te debería dar la medida de la figura en cuestión, claro está en que solo debe ir el jacobiano, esto te ayudará a saber si tal cambio de variable está bien hecho.
