Dadas las siguientes ecuaciones obtener la ecuación en forma canónica de las siguientes parábolas
Geometría
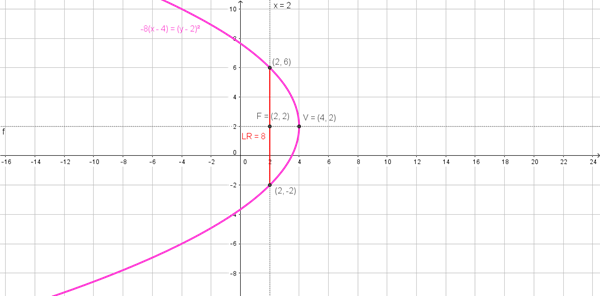
Obtener la ecuación en forma canónica de las siguientes parábolas. Además, determinar las coordenadas del vértice, del foco, de los extremos del lado recto y la longitud del lado recto. Dibuje la gráfica de cada parábola.
$$\begin{align}&y^2-4y+8x-28=0\end{align}$$$$\begin{align}&x^2+4x+16y+4=0\end{align}$$
1 Respuesta
Respuesta de Lucas m
1