Calcula la integral mediante sustitución trigonométrica

;)
Hola karla!

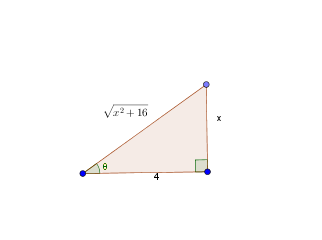
$$\begin{align}&tan \theta= \frac x 4 \\&\\&x=4 tan \theta\\&dx=4sec^2 \theta d  \theta\\&\\&\int  \frac 1 {\sqrt{x^2+16}}dx= \int  \frac 1 { \sqrt {(4 tan \theta)^2+16}}4 sec^2 \theta d \theta=\\&\\&4 \int  \frac 1 { \sqrt {16 tan^2 \theta+16}} sec^2 \theta d \theta=\\&\\&\frac 4 { \sqrt {16}} \int \frac 1 {\sqrt{tan^2 \theta +1}} sec^2 \theta d \theta=\\&\\&\frac 4 4 \int \frac 1 {\sqrt {sec^2 \theta}} sec^2 d \theta=\\&\\&\int \frac {sec^2 \theta}{sec \theta}d \theta= \int sec \theta d \theta= ln \Bigg|sec \theta+tan \theta \Bigg |==\\&\\&identidad \ trigonométrica:\\&sec^2 \theta= 1+ tan^2 \theta=1 + ( \frac x 4 )^2\\&\\&==ln \Bigg|  \sqrt { 1+ \frac{x^2}{16}}+ \frac x 4 \Bigg | + C\end{align}$$

La integral de la secante yome la sé como inmediata.

Si quieres saber de donde sale:

Procedimiento para obtener la integral de la secante

Otro procedimiento:

https://www.youtube.com/watch?v=J7EPDpCX4T4 

SAludos

;)

;)