Para la función dada determine la solución real del respectivo dominio y rango

;)
Hola omar!

Aclárame si es:

$$\begin{align}&1)\\&f(x)=x-7 \sqrt x -4\\&\\&o\\&esto\\&\\&2)\\&f(x)=x-7 \sqrt {x -4}\\&\end{align}$$

;)

;)

Ya que querés graficar, empecemos por ahí

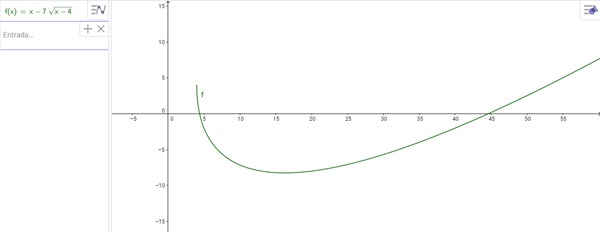
El dominio es 'fácil', porque como tenés una raíz par, el dominio va a estar dado por donde esté definida esta raíz y será cuando x-4 >= 0, o sea cuando x>=4

En la gráfica también se puede deducir el rango, pero calculémoslo a ver si llegamos a lo mismo :-)

$$\begin{align}&f(x) = x - 7 \sqrt{x-4}\\&\text{Hay dos formas, una es intentando despejar x de la función (pero no lo veo fácil)}\\&\text{Otra es analizar la derivada para ver donde es estrictamente creciente y/o decreciente}\\&f'(x) = 1-7 \cdot \frac{1}{2 \sqrt{x-4}}=1- \frac{7}{2 \sqrt{x-4}}\\&\text{Tiene el mismo dominio que f(x) así que no hay problemas por ese lado, veamos donde tiene un extremo local}\\&f'(x) =0 = 1- \frac{7}{2 \sqrt{x-4}}\\&7 = 2 \sqrt{x-4}\\&\frac{7}{2} = \sqrt{x-4}\\&\frac{49}{4} = x-4 \\&x = \frac{49}{4} + 4 = \frac{65}{4} = 16.25\\&\text{Por la gráfica sabemos que será mínimo, pero vamos a verificarlo con la derivada segunda}\\&f''(x) = \frac{7}{4 (x-4)^{3/2}}\\&\text{No es necesario calcularlo, alcanza con saber que f''(16.25) > 0, por lo tanto es mínimo}\\&\text{Como la función está definida en }[4,+\infty) \text{, es continua en todo su dominio y tiene un mínimo en x=16.25}\\&\text{Podemos asegurar que la función tiene los siguientes intervalos de crecimiento/decrecimiento}\\&Crece: (16.25,+\infty)\\&Decrece:(4,16.25)\\&\text{Veamos el intervalo que decrece, para eso evaluemos}\\&f(4) = 4-7 \sqrt{4-4}=4 \ (máximo\ local)\\&f(16.25) = 16.25-7 \sqrt{16.25-4}=-8.25 \text{ (como sabemos que la función luego crece, este es un mínimo absoluto)}\\&\text{En el intervalo que crece, ya tenemos el extremo izquierdo, falta calcular el límite en }+\infty\\&\lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} x - 7 \sqrt{x-4}=\lim_{x \to +\infty} (x - 7 \sqrt{x-4}) \cdot \frac{(x + 7 \sqrt{x-4})}{(x + 7 \sqrt{x-4})}=\\&\lim_{x \to +\infty}  \frac{x^2 - 49 (x-4)}{(x + 7 \sqrt{x-4})}=\lim_{x \to +\infty}  \frac{x^2(1 - \frac{49 (x-4)}{x^2})}{x(1 + \frac{7 \sqrt{x-4}}{x})}=\lim_{x \to +\infty}  \frac{x(1 - \frac{49 (x-4)}{x^2})}{(1 + \frac{7 \sqrt{x-4}}{x})}=+\infty \text{  (Como era esperable)}\\&\text{Por lo tanto, el rango es }[-8.25,+\infty)\end{align}$$

Salu2