¿Calcular longitud de la curva con funciones trascendentes?
Tengo que calcular la longitud de la curva, son mi ultima opción, ya probé con con cambio de variable, formula de la longitud de arco, derivar por regla de la cadena, y demás yerbas el problema:
Calcule la longitud de la curva
y=log(cos(x))
de x=-1.4 a x=0.4
2 Respuestas
·
·
¡Hola El Humano!
O estamos hablando de otro problema o dudo mucho que hayas resuelto este problema, porque la integral que sale no tiene función primitiva, es decir, no existe función elemental cuya derivada sea la integral que hay que calcular
La fórmula de la longitud del arco es:
$$\begin{align}&L=2\pi\int_a^bf(x)\sqrt{1+f'(x)^2}dx\\&\\&f(x)=log(\cos x)\qquad\text{logaritmo neperiano supongo}\\&\\&f'(x)=-\frac{sen\,x}{\cos x}=-tg \,x\\&\\&L=2\pi\int_{-1.4}^{0.4}log(\cos x) \sqrt{1+tg^2x}\;dx=\\&\\&2\pi\int_{-1.4}^{0.4}log(\cos x) \sqrt{sec^2x}\;dx=\\&\\&2\pi\int_{-1.4}^{0.4}log(\cos x) ·secx\;dx=\\&\\&2\pi\int_{-1.4}^{0.4}\frac{log(\cos x) }{\cos x}x\;dx=\end{align}$$Y aquí es donde hay que parar porque esa integral no puede calcularse. La solución es: o la integras tu mismo mediante algán algoritmo numerico como trapecios, Simpson, etc, o usas algún sofware que lo haga por ti.
Porque si intentas hacer la integral indefinida mira
Donde las Li2 son funciones especiales.
Por si necesitas más decimales, esto es lo que ha hecho Máxima:
El primer número es la respuesta, tampoco te fíes de todos los decimales que pone.
:
:
Y mil perdones. Debia estar traumatizado por el último problema de superficie de revolución y se me coló aqui la fórmula de una superficie de revolución. La fórmula de la longitud del arco también tiene la pesadilla de la integral de la raíz cuadrada pero es diferente. Voy a hacer bien el ejercicio.
$$\begin{align}&L=\int_a^b \sqrt{1+f'(x)^2}dx\\&\\&f(x)=log(\cos x)\qquad\text{logaritmo neperiano supongo}\\&\\&f'(x)=-\frac{sen\,x}{\cos x}=-tg \,x\\&\\&L=\int_{-1.4}^{0.4}\sqrt{1+tg^2x}\;dx=\\&\\&\int_{-1.4}^{0.4}\sqrt{sec^2x}\;dx=\\&\\&\int_{-1.4}^{0.4}secx\;dx=\end{align}$$Y en realidad esta integral es bastante complicada de resolver, lo que pasa es que no sabiendo por qué he visto que en algunos lugares la ponen en la tabla de inmediatas. Que quede bien claro, no es una integral inmediata por más que te la sepas de memoria o la puedas encontrar en un libro.
Aquí dejo el enlace de como se resuelve.
¿Cómo resolver la integral? Con procedimiento
Y una vez resuleta la indefinida ya solo hay que evaluar entre los extremos:
$$\begin{align}&ln\left|sec\,t+tg\,t \right|\bigg|_{-1.4}^{0.4}=\\&\\&ln|sec\,0.4+tg\,0.4| - ln|sec(-1.4)+tg(-1.4)|\approx \\&\\&2.86910981024158\\&\\&\end{align}$$Y eso es todo, espero que te sirva y lo hayas entendido. Perdón por el fallo primero.
Saludos.
:
:
Encontré la respuesta:
Primero estaba sustituyendo mal
Se sustituye la identidad de logaritmo por el coseno, de esta forma
1/cos(x)(-sin(x))
Después de eso se obtiene el resultado de la multiplicación
Y se sustituye en la integral de -1.4 a 0.9 se usa la formula de la curva √1-(f(x)')^2 y se evalúa y listo la respuesta la pongo por si alguien se quedo con al duda :)
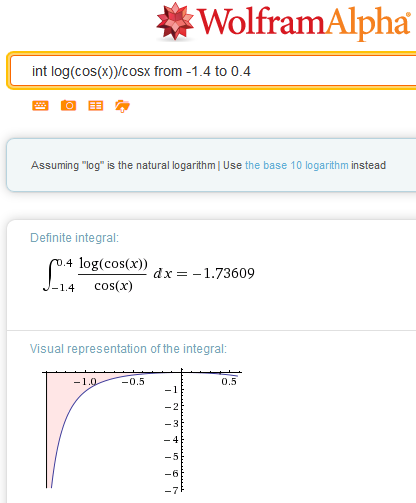
Profe, lo que no entiendo de la respuesta del Wolfran, es que supuestamente está calculando una longitud...que sentido tiene que el resultado sea negativo?. Saludos - Anónimo
Ya está corregido, gracias por avisarme, había usado la fórmula de la superficie de revolución en lugar de la longitud del arco, se que ambas son traumáticas y las tengo muy asociadas. - Valero Angel Serrano Mercadal