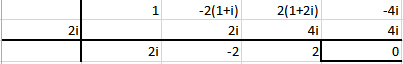¿Cómo resolver la siguiente ecuación?
1) resuelve en la ecuación: z^2-2z+2=0
2) sea P(Z)= z^3-2(1+i)z^2+2(1+2i)z-4i
a. Calcular P(2i)
b. Hallar a, b y c de modo que P(z)=(z-2i).(az^2+bz+c)
c. Deduce las raíces de P(Z)
2 Respuestas
Respuesta de Lucas m
1
Respuesta de Valero Angel Serrano Mercadal
1