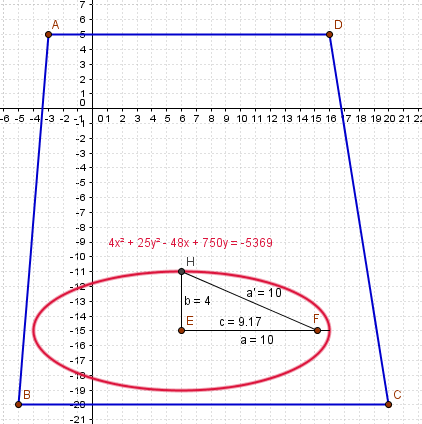
¿Cómo saco los semiejes de la siguiente elipse?
Planteamiento
El terreno está delimitado por los segmentos de recta que unen los vértices A, B, C y D. Construirás una alberca en forma de elipse con centro en el punto E de acuerdo a la siguiente figura:
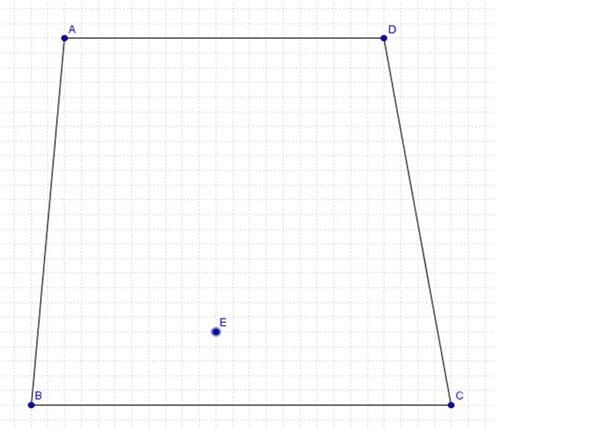
1.-basándote en las coordenadas del punto A escribe las coordenadas del punto E:
Coordenadas A (-3,5) E ( , )
DATOS
Orientación de la alberca: Horizontal
Valor del eje mayor = 20
Valor del eje menor = 8
2 .-Determina la ecuación ordinaria que representa el contorno de la alberca elíptica.
El valor del semieje mayor es: ¿?
El valor del semieje menor es: ¿?
El valor del semieje focal es: ¿?
La ecuación ordinaria de la elipse es: ¿?
3.- Convierte la ecuación de la forma ordinaria a la forma general.
1 respuesta
·
·
¡Hola Rocío!
No he entendido muy bien el planteamiento, veremos si haciendo los pasos que dicen es fácil.
1)
E está 9 a la derecha de A y 20 por debajo, eso es un vector (9, -20) que sumaremos al punto A
E = (-3, 5) + (9,-20) = (6, -15)
2)
Por decir que la orientación es horizontal el eje mayor irá en horizontal y el menor en vertical.
El semieje es la mitad del eje, luego:
Semieje mayor (a) = 20/2 = 10
Semieje menor (b) = 8/2 = 4 = b
El semieje focal (c) es la distancia del centro al foco y se calcula a partir de
b^2 + c^2 = a^2
c^2 = a^2 - b^2
c = sqrt(a^2-b^2) = sqrt(10^2 - 4^2) = sqrt(84) = 2·sqrt(21)
La ecuación ordinaria de la elipse es:
$$\begin{align}&\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1\\&\\&\text{Donde (h,k) es el centro, el punto E}\\&\\&\frac{(x-6)^2}{10^2}+\frac{(y+15)^2}{4^2}=1\\&\\&\text{o si acaso}\\&\\&\frac{(x-6)^2}{100}+\frac{(y+15)^2}{16}=1\end{align}$$3)
La pasamos a general.
$$\begin{align}&\frac{(x-6)^2}{100}+\frac{(y+15)^2}{16}=1\\&\\&\text{Lo mejr es tomar el mcm directamente}\\&\\&100=2^2·5^2\\&16=2^4\\&mcm(16,100)=2^4·5^2=16·25=400\\&\\&\frac{4(x-6)^2+25(y+15)^2}{400}=1\\&\\&4(x-6)^2+25(y+15)^2 = 400\\&\\&4x^2-48x+144+25y^2+750y+5625=400\\&\\&4x^2+25y^2-48x+750y+5369=0\end{align}$$Y uno no se queda conforme si no puede comprobar que se hizo bien el ejercicio.
Pues ha quedado perfecto, está bien la ecuación.
Y eso es todo.
Saludos.
:
:
