Necesito racionalizar este ejercicio de álgebra.
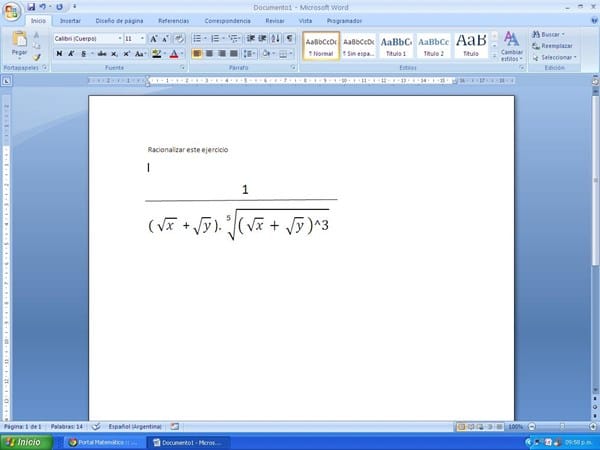
Amigos necesito me ayuden a racionalizar este ejercicio, envío una imagen del mismo.
Se que no es difícil pero me confunde la doble raíz que esta elevada a la quinta.
Gracias espero ayuda.
2 Respuestas
Respuesta de Valero Angel Serrano Mercadal
2
·
·
¡Hola Hfarias!
$$\begin{align}&\frac{1}{(\sqrt{x}+\sqrt{y}) \sqrt[5]{{(\sqrt{x}+\sqrt{y})^3}}}=\\&\\&\text{El racionalizador del primer factor es } \sqrt x-\sqrt y\\&\text{Y el del segundo es } \sqrt[5]{(\sqrt x+\sqrt y)^2}\\&\text{multiplicando y dividiendo por ambos}\\&\\&=\frac{(\sqrt x-\sqrt y)\sqrt[5]{(\sqrt x+\sqrt y)^2}}{(x-y)(\sqrt x + \sqrt y)}=\\&\\&\text{y el racionalizador del segundo del denominador es}\\&\sqrt x - \sqrt y\\&\text { multiplicamos y dividimos por él}\\&\\&=\frac{(\sqrt x-\sqrt y)^2\sqrt[5]{(\sqrt x+\sqrt y)^2}}{(x-y)(x -y)}=\\&\\&\frac{(\sqrt x-\sqrt y)^2\sqrt[5]{(\sqrt x+\sqrt y)^2}}{(x-y)^2}\\&\\&\end{align}$$Y eso es todo, saludos.
:
:
Respuesta
1
Veamos...
$$\begin{align}&\frac{1}{(\sqrt{x}+\sqrt{y}) \cdot \sqrt[5]{{(\sqrt{x}+\sqrt{y})^3}}}\\&\text{Para no confundirnos, escribamos la raíz y el exponente como}\\&\frac{1}{(\sqrt{x}+\sqrt{y}) \cdot {{(\sqrt{x}+\sqrt{y})^{3/5}}}}\\&\text{Ahora sabemos que }a^x \cdot a^y = a^{x+y}\\&\frac{1}{{{(\sqrt{x}+\sqrt{y})^{8/5}}}}\end{align}$$No se si a partir de ahí te arreglás o necesitás que siga con la racionalización
Estimado Omar puedes completarla, te lo agradecería.
a ver...
$$\begin{align}&\frac{1}{(\sqrt{x}+\sqrt{y})^{(8/5)}}=\\&\frac{1}{(\sqrt{x}+\sqrt{y})^{(8/5)}} \cdot \frac{(\sqrt{x}+\sqrt{y})^{(2/5)}}{(\sqrt{x}+\sqrt{y})^{(2/5)}}=\\&\frac{(\sqrt{x}+\sqrt{y})^{(2/5)}}{(\sqrt{x}+\sqrt{y})^{2}}\\&\text{Creo que ya lo podés dejar ahí, pero si quisieras hacer algo más podría ser...}\\&=\sqrt[5]{\frac{(\sqrt{x}+\sqrt{y})^{2}}{(\sqrt{x}+\sqrt{y})^{10}}}=\\&\sqrt[5]{\frac{1}{(\sqrt{x}+\sqrt{y})^{8}}}\\&\\&\\&\end{align}$$