Ejercicio de calculo integrales convergentes y divergentes
Requiero de resolver y graficar este ejercio de calculo integral, para saber si es convergente o divergente
1 Respuesta
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Juan!
Resolvamos la integral impropia por definición:
Espera, que esta integral y función tienen algo raro.
El dominio de la función es cuando el radicando es no negativa por ser una raíz cuadrada y cuando el denominador es distinto de 0 por ser un cociente. Entonces el dominio es
2-x >0
x < 2
Vale, el intervalo de integración está dentro del dominio, lo comprobé por si acaso.
$$\begin{align}&\int_{-\infty}^{-1}\frac{dw}{\sqrt{2-w}}=\lim_{R\to\infty} \int_{-R}^{-1}\frac{dw}{\sqrt{2-w}}=\\&\\&\text{la integral es fácil, no creo que necesites explicaciones}\\&\\&\lim_{R\to\infty} -2 \sqrt{2-w}\bigg|_{-R}^{-1} =\lim_{R\to\infty}-2(\sqrt 3-\sqrt{2+R})=\\&\\&-2(\sqrt 3- \sqrt{\infty}) =-2(-\infty) = \infty\end{align}$$Luego es divergente.
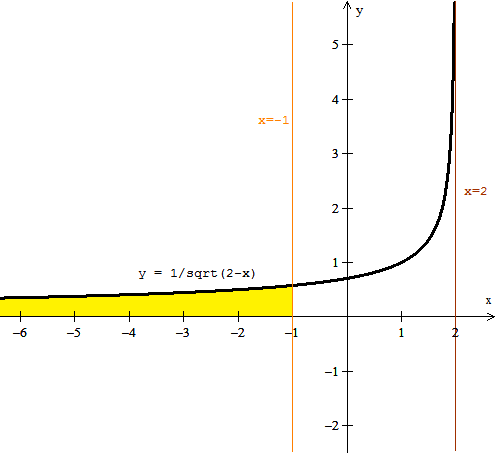
Y esta es la gráfica.
:
:
