Ejercicio de calculo integral(integrales trigonométricas)
Resolver el ejercicio de calculo integral, que dice como sigue, Evalúa la siguiente integral trigonométrica
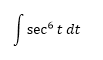
1 Respuesta
Respuesta de Valero Angel Serrano Mercadal
1
Se mandó sola la respuesta, la identidad es:
$$\begin{align}&sec^2x=1+tg^2x\\&\\&\text{Y recordar que }\\&\\&tg'(x)=sec^2(x) = 1+tg^2x\\&\\&\\&\\&\int sec^6 t\;dt=\int(1+tg^2t)^3dt=\\&\\&\int (1+tg^2t)^2·(1+tg^2t)dt=\\&\\&u=tg\,t\\&du=(1+tg^2t)dt\\&\\&\int(1+u^2)^2du=\int(1+2u^2+u^4)du=\\&\\&u+ \frac{2u^3}3+\frac{u^5}{5}+C=\\&\\&tg\,t+\frac{2\,tg^3t}{3}+\frac{tg^5t}{5}+C\\&\\&\end{align}$$:
:
