Evalúa cada uno de las siguientes integrales usando la formulación de integración por partes
Realiza el siguiente problema de calculo riferencial, Evalúa cada uno de las siguientes integrales usando la formulación de integración por partes
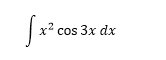
1 Respuesta
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Andrea!
Habrá que integrar do sveces para que desaparezca x^2
$$\begin{align}&\text{La fórmula de la integración por partes es:}\\&\int u\,dv = uv-\int v\,du\\&\\&\int x^2·\cos 3x\;dx=\\&\\&u=x^2\qquad\qquad\; du=2x\,dx\\&dv=\cos 3x \;dx\quad v=\frac 13 sen\, 3x\\&\\&=\frac 13 x^2 sen 3x-\frac 23\int x\,sen3x\;dx=\\&\\&u=x\qquad\qquad \quad du=dx\\&dv=sen\,3x\;dx\quad v=-\frac 13cos 3x\\&\\&=\frac 13 x^2 sen 3x+\frac 29x \cos 3x-\frac 29 \int \cos 3x dx=\\&\\&\frac 13 x^2 sen 3x+\frac 29x \cos 3x-\frac 2{27}sen\,3x+C\end{align}$$:
:
