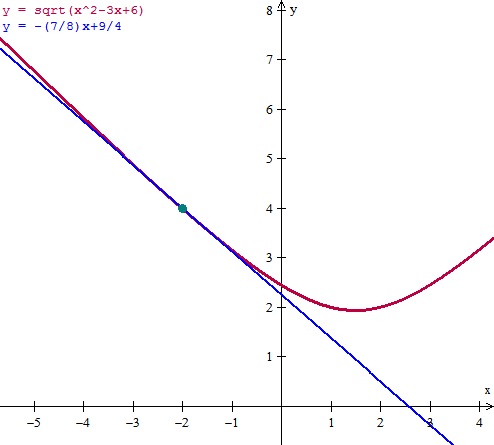
Halla la ecuación de la recta tangente a la curva
Buenas tardes ayuda con este punto gracias por su ayuda y dedicación
1 Respuesta
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Oscar!
La ecuación de la recta tangente a una curva f(x) en el punto (xo, yo) es
$$\begin{align}&y = y_0 + f'(x_0)(x-x_0)\\&\\&f(x)= \sqrt{x^2-3x+6}\\&\\&x_0=-2\\&\\&y_0=f(-2)= \sqrt{4+6+6}=4\\&\\&f'(x)=\frac{2x-3}{2 \sqrt{x^2-3x+6}}\\&\\&f'(x_0)=f'(-2)=\frac{2·(-2)-3}{2 \sqrt{4+6+6}}=-\frac 78\\&\\&\\&\text{Y la recta tangente es}\\&\\&y = 4 - \frac 78(x-(-2))\\&\\&y = 4 -\frac 78x-\frac 74\\&\\&y = -\frac 78x+\frac{9}{4}\end{align}$$Y la gráfca para comprobar que está bien es está:
:
:
