Calculo integral hallar el área bajo la curva

El área entre una función y eleje x se calcula:

$$\begin{align}&\Bigg | \int_a^b f(x)dx \Bigg |\\&\\&a \ y \ b \ son \ los \ puntos \ de \ corte \ con \ el \ eje \ X\\&\\&x^3-x^2-6x=0\\&x(x^2-x-6)=0\\&x_1=0\\&\\&x=\frac{1 \pm \sqrt {1+24}}{2}=\frac{1 \pm 5}{2}=\\&x_2=3\\&x_3=-2\\&\\&Hay \ tres \ puntos \ de \ corte \Rightarrow hay \ dos \ recintos:\\&\\&R_1= \int_{-2}^0(x^3-x^2-6x)dx= \Bigg[\frac{x^4}{4}-\frac{x^3}{3}-3x^2 \Bigg]_{-2}^0=\\&\\&=0-\Big(4+\frac{8}{3}-12)=\frac{16}{3}\\&\\&R_2= \Bigg |\int_{0}^{3}(x^3-x^2-6x)dx \Bigg |= \Bigg[\frac{x^4}{4}-\frac{x^3}{3}-3x^2 \Bigg]_{0}^{3}=\\&\\&=\Bigg |\frac{81}{4}-9-27 \Bigg |=\frac{63}{4}\\&\\&Area=\frac{63}{4}+\frac{16}{3}=\frac{253}{12}   =21.08333333... \ u^2\end{align}$$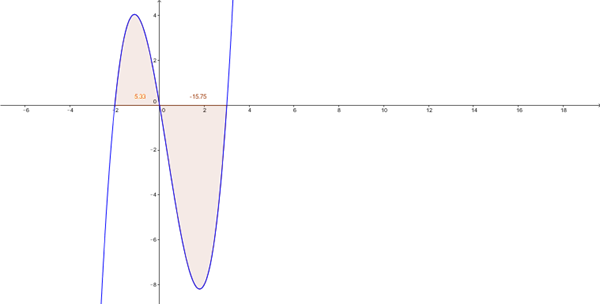

Saludos

;

;