Integración, determine el área de la región acotada por la curva

·

·

¡Hola Brenda!

Hay una y que no está muy claro si es conjunción o variable, yo creo que es conjunción.

Aunque no es difícil intuir la región a integrar haremos el dibujo

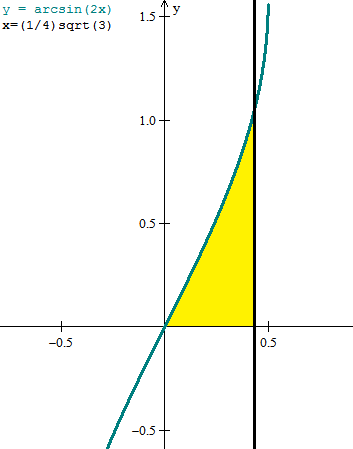
Luego el área es

$$\begin{align}&\int_0^{\sqrt 3/4}arcsen\,x\;dx=\\&\\&u= arcsen\,x\quad du=\frac{dx}{\sqrt {1-x^2}}\\&dv=dx\qquad\quad\; v=x\\&\\&x·arcsen \,x\bigg|_0^{\sqrt 3/4}- \int_0^{\sqrt 3/4} \frac{x\;dx}{\sqrt{1-x^2}}=\\&\\&\frac{\sqrt 3}{4}arc sen \frac{\sqrt 3}{4}- \int_0^{\sqrt 3/4} \frac{x\;dx}{\sqrt{1-x^2}}=\\&\\&t^2=1-x^2\\&2t\;dt=-2x\;dx\implies x\;dx=-t\;dt\\&x=0\implies t=1\\&x=\frac{\sqrt 3}{4}\implies t=\sqrt{1-\frac{3}{16}}=\frac{\sqrt{13}}{4}\\&\\&=\frac{\sqrt 3}{4}arc sen \frac{\sqrt 3}{4}+\int_1^{\sqrt {13}/4}\frac{t\;dt}{t}=\\&\\&\frac{\sqrt 3}{4}arc sen \frac{\sqrt 3}{4}+t\bigg|_1^{\sqrt {13}/4}=\\&\\&\frac{\sqrt 3}{4}arc sen \left(\frac{\sqrt 3}{4}\right)+\frac{\sqrt{13}}{4}-1\approx 0.095304935\\&\\&\\&\\&\\&\end{align}$$

:

: