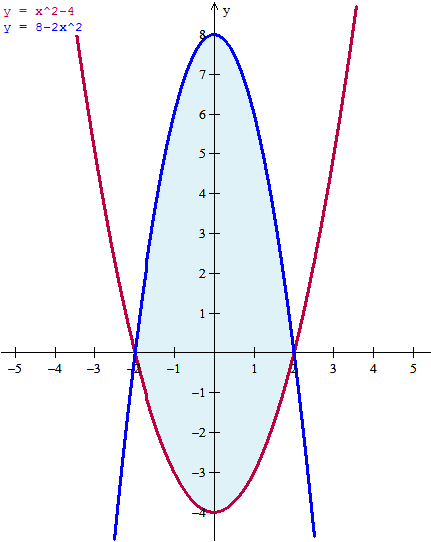
Determinar el área de la región limitada por las curvas dadas: y=x^2-4, y=8-2x^2
Por favor me pueden ayudar a determinar el área de la región limitada por las curvas dadas: y=x^2-4, y=8-2x^2 Realizando la gráfica y la integral
1 Respuesta
Respuesta de Valero Angel Serrano Mercadal
1