¿ Quién sabe hacer demostraciones vectoriales ?
En un paralelogramo ABCD, si M, N son puntos medios de AB y CD, respectivamente, demuestre vectorialmente que AMCN es un paralelogramo.
En un triangulo ABC, M,N,R son los puntos medios de AB, BC,CA, respectivamente. Demuestre que AN +BR+CM=0.
1 respuesta
Respuesta de Lucas m
1
Juan Esteban Rodas!
1) Observa el paralelogramo
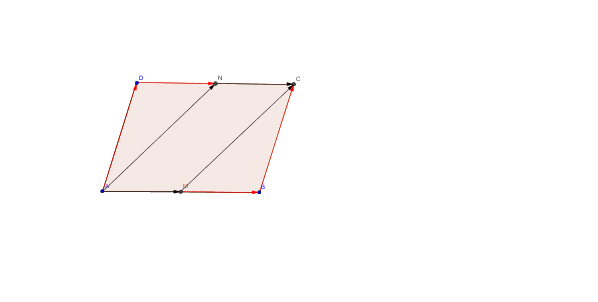
$$\begin{align}&\vec{AM}= \frac{1}{2}\vec{AB}\\ &\\ &\vec{NC}=\frac{1}{2} \vec{DC}\\ &\\ &Como \ se \ cumple \ \vec{AB}=\vec{DC}\\ &\\ &\Rightarrow \vec{AM}=\vec{NC}\\ &\\ &Por \ otro \ lado:\\ &\vec{MC}=\vec{MB}+\vec{BC}=\frac{1}{2} \vec{AB}+\vec{BC}\\ &\\ &y \\ &\\ &\vec{AN}=\vec{AD}+\vec{DN}=\vec{AD}+\frac{1}{2}\vec{DC}\\ &\\ &y \ siendo \ \vec{AD}=\vec{BC}\\ &y\\ &\vec{AB}=\vec{DC} \Rightarrow \vec{AN}=\vec{MC}\\ &\\ &Luego \ es \ un \ paralelogramo.\\ &\\ &2.- Ver \ figura\\ &\\ &\vec{AN}+\vec{BR}=(\vec{AB}+\vec{BN})+(\vec{BA}+\vec{AR)}=\\ &\vec{BN}+\vec{AR}=\vec{BN}+\vec{MN}(paralela \ media)=\\ &\vec{NC}+\vec{MN}=\vec{MC}\\ &\\ &Luego:\\ &\vec{AN}+\vec{BR}+ \vec{CM}=\vec{MC}+\vec{CM}= \vec{0}\\ &\\ &\end{align}$$Recuerda que al sumar vectores opuestos AB+BA=0
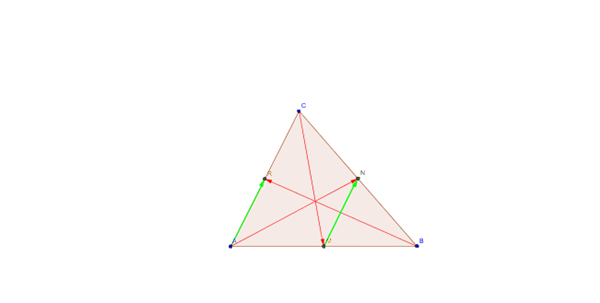
Espero que te sirva y que lo hayas entendido
Un placer.
Recuerda votar, es lo único que se pide en este chat.
Excelente es lo correcto.
