¿Aplicaciones de los vectores a la física?

Es verdad que la Física se me da mal, pero algo si puedo hacer.

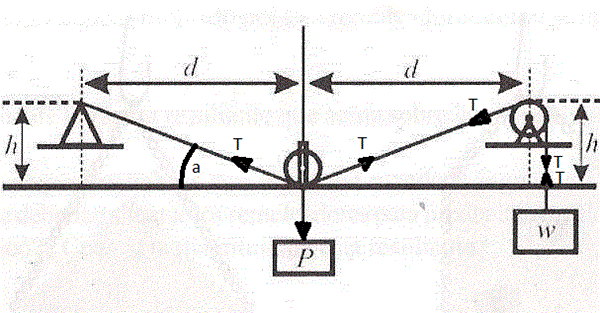
El dibujo ya se que está muy mal pero es muy difícil dibujar con el TouchPad del portátil.

Haciendo el corte imaginario del objeto de peso P nos quedan dos fuerzas de tensión y P.

Como el objeto está en equilibrio el sumatorio de esta fuerzas será cero y será cero en los dos ejes.

El ángulo a que he mal dibujado, es el ángulo cuya tangente vale h/d. Lo que nos interesa es conocer el seno para descomponer las dos fuerzas T en el eje Y

$$\begin{align}&\frac{sena}{cosa}= \frac hd\\ &\\ &\frac{sena}{\sqrt{1-sen^2a}}=\frac hd\\ &\\ &\frac{sen^2a}{1-sen^2a}= \frac {h^2}{d^2}\\ &\\ &sen^2a=\frac {h^2}{d^2} - \frac {h^2}{d^2} sen^2a\\ &\\ &\left( 1+ \frac {h^2}{d^2} \right)sen^2a=\frac {h^2}{d^2}\\ &\\ &sen^2a = \frac{\frac {h^2}{d^2}}{1+\frac {h^2}{d^2}}=\frac{h^2}{h^2+d^2}\\ &\\ &sena=\frac{h}{\sqrt{h^2+d^2}}\\ &\end{align}$$

La componente en Y de cada fuerza T será el módulo de T por ese seno que hemos calculado. Dos veces esa componente Y será igual a la fiurza P

Con esto vamos a poder calcular el módulo de T

$$\begin{align}&2T·\frac{h}{\sqrt{h^2+d^2}}=P\\ &\\ &\\ &T=\frac{P \sqrt{h^2+d^2}}{2h}\\ &\end{align}$$

Y con este valor de T vamos a la parte derecha donde tenemos el objeto de peso W con la fuerza de ese peso y la tensión. Solo hay fuerzas en el eje Y y deben contrarrestarse.

Es tan sencillo que no hay que hacer más cuentas, el resultado es:

$$\begin{align}&W= \frac{P \sqrt{h^2+d^2}}{2h}\\ &\end{align}$$

Y eso es todo, espero que te sirva y lo hayas entendido. La verdad es que no conozco a ningún experto en Física, una vez tenía una pregunta que hice y no contestó nadie.