Hallar el radio r de la esfera inscrita en lapirámide.
En una pirámide regular cuadrangular, la arista de la base tiene longitud a y las áreas de las caras laterales son iguales al área de la base. Hallar el radio r de la esfera inscrita en la pirámide.
Este ejercicio me resulta tremendamente parecido a otro que resolví, deja que lo busque para ponerlo.
Problema de geometría hallar área y volumen de la esfera
Míralo un poco para ver si te sirve lo que hice o no . Ahora no puedo dedicarme con detenimiento este ejercicio, lo haré más tarde.
Sa lu dos.
:
:
El ángulo JEO es la mitad del JEG ya que es EO es la bisectriz del ángulo. Dadas dos tangentes a una circunferencia la bisectriz pasa por el centro de la circunferencia. Luego nos interesa conocer el ángulo JEG, que es un ángulo cuya tangente mide la altura de la pirámide entre la mitad de un arista
tg(JEG) = h/(a/2) = 2h/a
Para calcular h llamemos V al vértice superior, entonces
$$\begin{align}&\overline{EV} = a·\cos 60º\\&\\&\overline{EV}^2 = h^2 + \left(\frac a2\right) ^2\\&\\&h= \sqrt{\overline{EV}^2-\left(\frac a2\right) ^2}=\\&\\&\sqrt{a^2cos^2 60º-\frac{a^2}4}=\\&\\&a \sqrt {\frac 34-\frac 14}=\frac a{\sqrt 2}=\frac{\sqrt{2}}{2}a\\&\\&Luego\\&\\&tg(JEG)= \frac{2·\frac{\sqrt{2}}{2}a}a=\sqrt 2\\&\\&ang(JEG)= arctg \sqrt 2 \\&\\&ang(JEO)=\frac{arctg \sqrt 2}{2}\\&\\&tg(JEO)=\frac r{\frac a2}\\&\\&r= \frac a2·tg(JEO)\\&\\&r=\frac a2·tg\left(\frac{arctg \sqrt 2}{2} \right)=\\&\\&\frac a2·0.5176380902=\\&\\&0.2588190451a\\&\\&\end{align}$$Compruebo que la respuesta es distinta de Lucas. Una vez mandada la repasaré porque se analiza mejor si se puede ver en conjunto. Dentro de un rato la confirmo o me desdigo.
Saludos.
:
:
Donde puse cos(60º) quería decir sen(60º) pero no altera el resultado porque los valores que puse son los de sen(60º)
$$\begin{align}&\overline{EV} = a·sen\, 60º\\&\\&\overline{EV}^2 = h^2 + \left(\frac a2\right) ^2\\&\\&\\&h= \sqrt{\overline{EV}^2-\left(\frac a2\right) ^2}=\\&\\&\sqrt{a^2sen^2 60º-\frac{a^2}4}=\\&\\&a \sqrt {\frac 34-\frac 14}=\frac a{\sqrt 2}=\frac{\sqrt{2}}{2}a\\&\\&Luego\\&\\&tg(JEG)= \frac{2·\frac{\sqrt{2}}{2}a}a=\sqrt 2\\&\\&ang(JEG)= arctg \sqrt 2 \\&\\&ang(JEO)=\frac{arctg \sqrt 2}{2}\\&\\&tg(JEO)=\frac r{\frac a2}\\&\\&r= \frac a2·tg(JEO)\\&\\&r=\frac a2·tg\left(\frac{arctg \sqrt 2}{2} \right)=\\&\\&\frac a2·0.5176380902=\\&\\&0.2588190451a\\&\\&\end{align}$$Pues yo pienso que mi respuesta está bien.
Saludos.
:
:
Y lo confirmo con esta imagen que es la proyección de la pirámide y esfera
El radio mide 0.2588190451a
Vale, me confundí yo, tomé como pirámide regular la que tiene triángulos equiláteros en los lados y no es eso, tiene triángulos isósceles todos iguales.
Primero calculamos la altura de dichos triángulos usando lo que nos dicen del área.
El área de la base es
Ab= a^2
Y la de los triángulos laterales
At = a·h/2
a^2 = ah/2
2a^2 = ah
h = 2a
Esta h es el VE del dibujo donde V es el punto de arriba.
Entonces el coseno del ángulo JEV es
cos(JEV) = (a/2) / (2a) = 1/4
Y el ángulo JEO es la mitad de JEV por EG y EJ tangentes a la esfera.
Dado el coseno de un ángulo la tangente del ángulo mitad es:
$$\begin{align}&tg \frac x2= \pm \sqrt{\frac{1-\cos x}{1+cosx}}\\&\\&tg(JEO)= \sqrt{\frac{1-\frac 14}{1+\frac 14}}=\sqrt{\frac 35}\\&\\&Tenemos \\&\\&\frac{\overline{OJ}}{\overline{JE}}=tg(JEO)\\&\\&\frac r{\frac a2}= \sqrt{\frac 35}\\&\\&r= \frac a2 \sqrt{\frac 35}= \frac{a \sqrt{15}}{10}\end{align}$$Vale, ahora si que coincidimos aunque los cálculos hayan sido distintos. Y la comprobación demuestra que está bien
Y eso es todo, perdona por el fallo.
1 respuesta más de otro experto
;)
Hola Alvaro Vargas!
AB=a
JE= a/2
área base=area triángulo lateral
$$\begin{align}&a^2=\frac{VE·BC}{2}=\frac{VE·a}{2}\\&\\&\overline{VE}=2a\end{align}$$Los triángulos VOG y VEJ son semejantes, al tener los tres ángulos iguales
ánguloOVG=ánguloJVE por ser común en el vértice (V)
angulo VGO= angulo VJE = 90º
Luego el ángulo que falta tambien seran iguales (suman 180º)
Establecemos las equivalencias:
$$\begin{align}&\frac{VO}{VE}=\frac{OG}{EJ}\\&\\&sea H=VJ\\&VO=VJ-OJ=H-r\\&\\&\frac{H-r}{2a}=\frac{r}{a/2}\\&\\&(H-r) \frac{a}{2}=2ar\\&\\&\frac{aH}{2}=2ar+\frac{ar}{2}\\&\\&\frac{aH}{2}=\frac{5ar}{2}\\&\\&r=\frac{H}{5}\\&\\&\\&Pitágoras \ en \ triángulo \ VJE:\\&VE^2=VJ^2+JE^2\\&\\&VJ^2=VE^2-JE^2\\&\\&H^2=(2a)^2-(\frac{a}{2})^2\\&\\&H^2=4a^2-\frac{a^2}{4}=\frac{15a^2}{4}\\&\\&H=\frac{a}{2} \sqrt {15}\\&\\&r=\frac{H}{5}=\frac{a}{10} \sqrt {15}\end{align}$$saludos
;)
;)
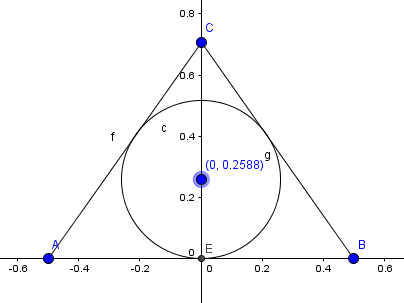
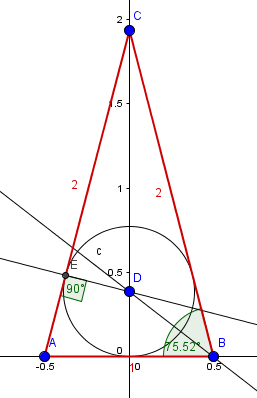
;)Hola profesor Valero,¿de donde sale el ángulo de 60º?Saludos - Lucas m
Una pirámide cuadrangular regular tiene cuatro triángulos equiláteros como caras, entonces la altura de cada uno de ellos es el lado por el seno de 60º - Valero Angel Serrano Mercadal
Una pirámide cuadrangular regular , tengo entendido que es la que la base es un polígono regular, las caras son triángulos isósceles de ahí el ato del área lateral. Bueno yo así le tengo entendidohttps://es.wikipedia.org/wiki/Pir%C3%A1mide_(geometr%C3%ADa) Respetuosamente. SAludos - Lucas m
Tienes razón, no se de dónde saqué eso. Cuando tenga tiempo lo corrijo, estoy muerto. - Valero Angel Serrano Mercadal
Gracias por advertirme del fallo, ya lo corregí y me da lo mismo que a ti con un método distinto. - Valero Angel Serrano Mercadal
Saludos - Lucas m