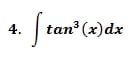Quien gana haber calculo física matemáticas
Hola hola hola hola hola hola hola hola hola hola hola hola hola hola hola hola
2 Respuestas
·
·
¡Hola Esneider!
$$\begin{align}&\int tg^3x\;dx=\\&\\&t=tg\,x\\&dt=(1+tg^2x)dx\implies dx= \frac{dt}{1+tg^2x}=\frac{dt}{1+t^2}\\&\\&=\int \frac{t^3}{1+t^2}dt=\\&\\&\text{haciendo la división entera de polinomios}\\&\\&= \int \left( t - \frac{t}{1+t^2}\right)dt = \frac {t^2}2-\int \frac{t}{1+t^2}dt=\\&\\&\frac {t^2}2-\frac 12ln(1+t^2)+C=\\&\\&\frac{tg^2x-ln(1+tg^2x)}{2}+C\\&\\&\text{Bueno, atención porque hay mil formas de expresar la integral}\\&\\&\text{Ya que } 1+tg^2x=sec^2x \text{ se puede poner como} \\&\\&\frac{tg^2x - ln(sec^2x)}{2}+C= \frac{tg^2x-2ln(sec\,x)}{2}+C=\\&\\&\frac{tg^2x}{2}-ln(sec\,x)+C=\frac{tg^2x}{2}+ln(\cos x)+C\\&\\&\text{Pero también se puede llegar a}\\&\\&\frac{sec^2x-1}{2}+ln\,x+C=\frac{sec^2x}{2}-\frac 12+ln\,x+C=\\&\\&\text{y como solo necesitamos una constante genérica}\\&\\&\frac{sec^2x}{2}+ln\,x+C=\end{align}$$Luego fíjate en eso, que muchas veces lo que tu hagas o lo que te den algunos programas parece que no es lo mismo pero es lo mismo o en todo caso es lo mismo más una constante. Y eso es todo, saludos.
:
:
¡Gracias!
muchas gracias sos el mejor.
Pero aunque sea el mejot me confundo muchas veces.
La parte final es:
$$\begin{align}&\text{Pero también se puede llegar a}\\&\\&\frac{sec^2x-1}{2}+ln\,(\cos x)+C=\frac{sec^2x}{2}-\frac 12+ln\,(\cos x)+C=\\&\\&\text{y como solo necesitamos una constante genérica}\\&\\&\frac{sec^2x}{2}+ln\,(\cos x)+C\end{align}$$Conste que mi primera intención era hacerla sumando y restando tgx, tal como la ha hecho el otro experto, pero me pareció demasiado artificial y preferí hacerlo con cambio de variable que es lo típico.
La integral planteada se puede resolver de forma muy sencilla desglosándola de la siguiente forma:
$$\begin{align}&\int\tan^3(x)dx=\int\tan^2(x)\cdot \tan(x)dx=\int(1+\tan^2(x)-1)\cdot \tan(x)dx=\int(1+\tan^2(x))\cdot \tan(x)dx-\int\tan(x)dx\end{align}$$Sabiendo que la derivada de la tangente es 1+(tan^2(x)), la primera integral entonces es inmediata, de resultado (tan^2(x))/2 (si no lo ves puedes realizar el cambio tan(x)=u y comprobarlo). En cuanto a la segunda, se puede resolver aplicando la definición de tangente de x en función del seno y coseno, teniendo en realidad la integral:
$$\begin{align}&\int\frac{\sin(x)}{\cos(x)}dx\end{align}$$Vemos que, dado que la derivada del coseno es justo -sin(x), tenemos un resultado logarítmico:
$$\begin{align}&\int\frac{\sin(x)}{\cos(x)}dx=-\ln(\cos(x))+cte\end{align}$$(Si no lo ves claro, puedes realizar el cambio de variable u=cos(x) y comprobarlo). Ha de tenerse en cuenta que el logaritmo sólo está definido para valores positivos del coseno.Por último, el resultado final de esta integral , teniendo en cuenta que el segundo sumando tiene un signo negativo delante, es:
$$\begin{align}&\int\tan^3(x)dx=\frac{\tan^2(x)}{2}+\ln(\cos(x))+cte\end{align}$$