Como se puede resolver un ejercicio de geometría analítica

Si por supuesto, te decía de hacerlo en geogebra para que entiendas lo que te están pidiendo. Lo que tienes que hacer es plantear la ecuación de la circunferencia, y luego como te dan el valor de la ordenada, reemplazas en la expresión anterior el valor de y por 8 para despejar el valor de x, si encuentras un valor (lo hallarás) ya puedes armar el punto B.

Veamos:

Ecuación de la circunferencia: (x - x_0)^2 + (y - y_0)^2 = r^2

(x-6)^2 + (y+4)^2 = 12^2

Despejamos y por 8 para despejar x

(x-6)^2 + (8+4)^2 = 12^2

(x-6)^2 = 0

x-6 = 0

x = 6

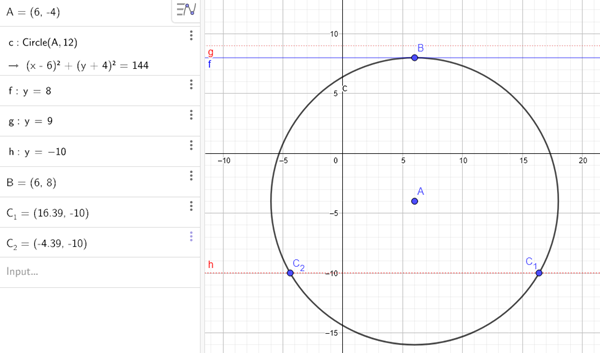
O sea que el punto B está en (6,8)

Para que quede más claro este punto, veamos otros casos de ordenada

y = 9

(x-6)^2 + (9+4)^2 = 12^2

(x-6)^2 = -25

(x-6) = Raiz(-25)

No tiene solución

y = -10

(x-6)^2 + (-10+4)^2 = 12^2

(x-6)^2 = 108

x-6 = Raiz(108)

x = 6 +/-  6Raiz(3)

x_1 = 6 (1 + Raiz(3)) APROX 16.39

x_2 = 6 (1 - Raiz(3)) APROX -4.39

En este caso hay 2 puntos

C_1 = (16.39, -10)

C_2 = (-4.39, -10)

Igualmente te dejo la gráfica, que generalmente sirve mucho para entender de que se trata