Calcule el área dadas las parábolas y^2=x^2/3 y h(x)=-x^2+4x

Más allá que en este caso te lo están pidiendo explicitamente, siempre que se pueda en estos casos conviene empezar por el gráfico, para intentar entender cual es el problema que plantean...

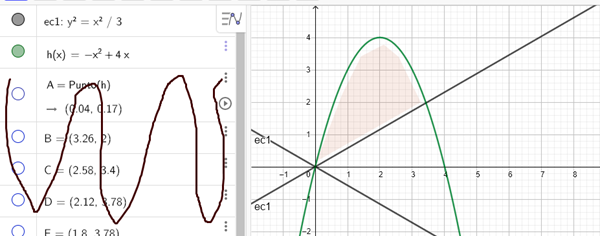
Dice el área límitada, así que supongo que es esa región que sombreé, donde vemos que la curva h(x) está por encima de la otra. Vemos que el primer punto del intervalo es x=0, falta ver el segundo punto, que por la gráfica parece ser 3.5, pero por supuesto que debemos calcular explicitamente para estar seguros... para eso planteamos

$$\begin{align}&ec1 = h(x), o sea\\&\frac{x^2}{3}=(-x^2+4x)^2\\&\frac{x}{\sqrt{3}}=-x^2+4x\\&\frac{\sqrt{3} x}{3}=-x^2+4x\\&0 = -x^2+4x-\frac{\sqrt{3} x}{3}\\&0 = x(-x+\frac{12-\sqrt{3} }{3})\\&x=0 \text{Ya lo sabíamos)}\\&x= \frac{12 - \sqrt{3}}{3}\\&\text{Menos mal que lo calculamos porque ese número claramente no es 3.5}\\&A = \int_0^{\frac{12 - \sqrt{3}}{3}}(-x^2+4x) - (\frac{\sqrt{x^2}}3) dx = \\&\int_0^{\frac{12 - \sqrt{3}}{3}}(-x^2+4x - \frac{x \sqrt{3}}3) dx = \\&\end{align}$$

Te dejo el cálculo de la integral, ya que son primitivas de polinomios...

Salu2