Puesto que el punto (3,2) divide al segmento de recta determinado por los puntos: P1(2,4) y P2(x2,y2) en la relación r = 3/2,

Lo primero que te recomiendo es que hagas una imagen para esquematizar lo que están preguntando (dibujé los puntos y la recta que pasa entre los mismos...)

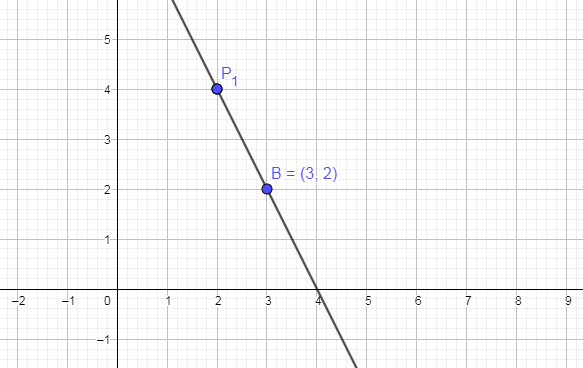
Vemos que el punto (4,0) sería el opuesto a P1 y si este fuera el caso, la relación sería 1/1. Como la relación es 3/2, entonces el punto en cuestión tiene que estar sobre la recta, pero entre el punto B el el punto (4,0) (**)

Todo lo anterior fue porque no sé si hay una manera 'automática' de resolver este ejercicio, así que lo voy a ir haciendo sin ninguna receta.

Lo primero que voy a hacer es calcular la ecuación de esa recta (que pasa por P1, B) y es

$$\begin{align}&\frac{y-4}{2-4}=\frac{x-2}{3-2}\\&y = -2x+8\end{align}$$

Vemos que entre P1 y el punto B, la relación es 3 y que entre B y P2 hay 2, así que en el eje 'X' la diferencia entre P1 y B la partimos entre 3 (lo que da un tercio) y luego la multiplicamos por 2 (lo que da 2/3).

Así que la componente 'X' del punto P2 será el la componente 'X' del punto B más 2/3. Para calcular la componente 'Y', simplemente reemplazamos el valor de X en la ecuación de la recta que hallamos

$$\begin{align}&x_{P2}=x_B + \frac{2}{3}=3+\frac{2}{3}=\frac{11}{3}\\&y_{P2}=-2\cdot x_{P2} + 8=-2 \cdot \frac{11}{3}+8=\frac{2}{3}\end{align}$$

Por lo que P2 = (11/3 ; 2/3)

Vemos que se cumple lo que habíamos dicho en (**), ahora veamos el punto en el gráfico anterior...

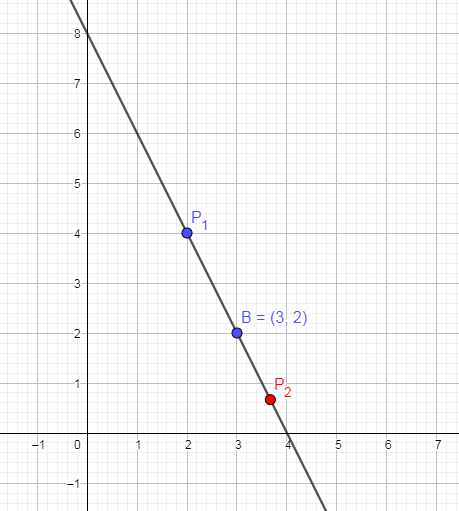
Salu2

Sea P = (3,2) entonces 

$$\begin{align}&\overrightarrow{P_1P}=r\cdot \overrightarrow{P P_2}\\&\\&\\&\overrightarrow{P_1P}=\frac{3}{2}\cdot \overrightarrow{P P_2}\\&\\&2\overrightarrow{P_1P}=3 \overrightarrow{P P_2}\\&\\&2(P-P_1)=3(P_2-P)\\&\\&3P_2=5P-2P_1\\&\\&3P_2=5(3,2)-2(2,4)\\&\\&3P_2=(15,10)-(4,8)\\&\\&3P_2=(11,2)\\&\\&P_2=\left(\frac{11}{3},\frac{2}{3}\right)\end{align}$$